��Ŀ����
��ƽ��ֱ������ϵ�У����Dz����Ѻ���������������ȵĵ��Ϊ����֮�㡱������㣨��1����1������0��0������ ��
�� ���������ǡ���֮�㡱����Ȼ�������ġ���֮�㡱����������
���������ǡ���֮�㡱����Ȼ�������ġ���֮�㡱����������
��1������P��2��m���Ƿ���������y=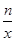 ��nΪ������n��0����ͼ���ϵġ���֮�㡱������������������Ľ���ʽ��
��nΪ������n��0����ͼ���ϵġ���֮�㡱������������������Ľ���ʽ��
��2������y=3kx+s��1��k��s�dz�������ͼ���ϴ��ڡ���֮�㡱�������ڣ����������֮�㡱�����ꣻ�������ڣ���˵�����ɣ�
��3�������κ���y=ax2+bx+1��a��b�dz�����a��0����ͼ���ϴ���������ͬ�ġ���֮�㡱A��x1��x1����B��x2��x2���������㩁2��x1��2��|x1��x2|=2����t=b2��2b+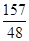 �������t��ȡֵ��Χ��
�������t��ȡֵ��Χ��
��1��y= ����2����k��
����2����k�� ʱ������֮�㡱������Ϊ��
ʱ������֮�㡱������Ϊ��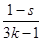 ��
��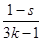 ������k=
������k= ��s=1ʱ������֮�㡱������������k=
��s=1ʱ������֮�㡱������������k= ��s��1ʱ�������ڡ���֮�㡱����3��t��
��s��1ʱ�������ڡ���֮�㡱����3��t�� ��
��
���������������1�����ɡ���֮�㡱�Ķ���ó�m=2���ٽ���P�������y=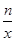 �����ô���ϵ����������������������Ľ���ʽ��
�����ô���ϵ����������������������Ľ���ʽ��
��2�����躯��y=3kx+s��1��k��s�dz�������ͼ���ϴ��ڡ���֮�㡱��x��x��������x=3kx+s��1�������ã�3k��1��x=1��s���ٷ���������������ۼ��ɣ�
��3���Ƚ�A��x1��x1����B��x2��x2������y=ax2+bx+1���õ�ax12+��b��1��x1+1=0��ax22+��b��1��x2+1=0�����ݷ��̵Ľ�Ķ����֪x1��x2��һԪ���η���ax2+��b��1��x+1=0�����������ɸ���ϵ���Ĺ�ϵ�ɵ�x1+x2= ��x1•x2=
��x1•x2= ����x1��x2��2=��x1+x2��2��4x1•x2=
����x1��x2��2=��x1+x2��2��4x1•x2= =4�������ó�b2��2b=��2a+1��2��2����t=b2��2b+
=4�������ó�b2��2b=��2a+1��2��2����t=b2��2b+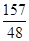 =��2a+1��2+
=��2a+1��2+ �����ɩ�2��x1��2��|x1��x2|=2���ó���4��x2��4����8��x1•x2��8������8��
�����ɩ�2��x1��2��|x1��x2|=2���ó���4��x2��4����8��x1•x2��8������8�� ��8����a��0���ⲻ��ʽ��ó�a��
��8����a��0���ⲻ��ʽ��ó�a�� ���������t��ȡֵ��Χ��
���������t��ȡֵ��Χ��
�����������1���ߵ�P��2��m���ǡ���֮�㡱��
��m=2��
�ߵ�P��2��2���ڷ���������y=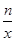 ��nΪ������n��0����ͼ���ϣ�
��nΪ������n��0����ͼ���ϣ�
��n=2��2=4��
�෴���������Ľ���ʽΪy= ��
��
��2�����躯��y=3kx+s��1��k��s�dz�������ͼ���ϴ��ڡ���֮�㡱��x��x����
����x=3kx+s��1��
�������ã�3k��1��x=1��s��
��3k��1��0����k�� ʱ�����x=
ʱ�����x=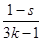 ��
��
��3k��1=0��1��s=0����k= ��s=1ʱ��x�������⣻
��s=1ʱ��x�������⣻
��3k��1=0��1��s��0����k= ��s��1ʱ��x�⣻
��s��1ʱ��x�⣻
������������k�� ʱ������֮�㡱������Ϊ��
ʱ������֮�㡱������Ϊ��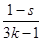 ��
��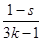 ������k=
������k= ��s=1ʱ������֮�㡱������������k=
��s=1ʱ������֮�㡱������������k= ��s��1ʱ�������ڡ���֮�㡱��
��s��1ʱ�������ڡ���֮�㡱��
��3���߶��κ���y=ax2+bx+1��a��b�dz�����a��0����ͼ���ϴ���������ͬ�ġ���֮�㡱A��x1��x1����B��x2��x2����
��x1=ax12+bx1+1��x2=ax22+bx2+1��
��ax12+��b��1��x1+1=0��ax22+��b��1��x2+1=0��
��x1��x2��һԪ���η���ax2+��b��1��x+1=0����������ʵ����
��x1+x2= ��x1•x2=
��x1•x2= ��
��
�ࣨx1��x2��2=��x1+x2��2��4x1•x2=�� ��2��4��
��2��4�� =
= =4��
=4��
��b2��2b=4a2+4a��1=��2a+1��2��2��
��t=b2��2b+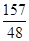 =��2a+1��2��2+
=��2a+1��2��2+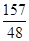 =��2a+1��2+
=��2a+1��2+ ��
��
�ߩ�2��x1��2��|x1��x2|=2��
�ੁ4��x2��0��0��x2��4��
�ੁ4��x2��4��
�ੁ8��x1•x2��8��
�ੁ8�� ��8��
��8��
��a��0��
��a��
�ࣨ2a+1��2+ ��
�� +
+ =
= ��
��
��t�� ��
��
���㣺���κ����ۺ��⣮

 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д� �����壬��˫����
�����壬��˫���� ��������
�������� �Ľ����ڵ��� �����ޣ�
�Ľ����ڵ��� �����ޣ�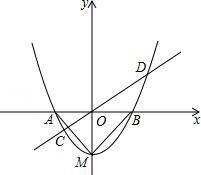
 �У�
�� ��
�� ��������
�������� �ֱ��ڱ�
�ֱ��ڱ� �ϻ�������
�ϻ������� ����
���� ��������������
Ϊ��������������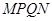 ������߳�Ϊ
������߳�Ϊ ��������
�������� ��
�� �ϸ�
�ϸ� ��
��  ʱ��
ʱ�� ǡ�����ڱ�
ǡ�����ڱ� ����
����

 x2+
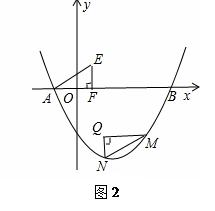
x2+ x��2��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C���ֱ����B��C��y�ᣬx���ƽ���ߣ���ƽ���߽��ڵ�D������BDC�Ƶ�C��ʱ����ת��ʹ��D��ת��y���ϵõ���FEC������BF��
x��2��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C���ֱ����B��C��y�ᣬx���ƽ���ߣ���ƽ���߽��ڵ�D������BDC�Ƶ�C��ʱ����ת��ʹ��D��ת��y���ϵõ���FEC������BF��
 ��x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC��
��x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC��
 �У����κ���
�У����κ��� ��
��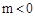 ����ͼ����
����ͼ���� �������ύ��A�㣮
�������ύ��A�㣮 ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
 ����A��-1��0����C��3��-2�����㣬��
����A��-1��0����C��3��-2�����㣬�� �ύ�ڵ�D����
�ύ�ڵ�D���� �ύ����һ��B��
�ύ����һ��B�� ��
�� �����ı���ABCD������ȷ֣���
�����ı���ABCD������ȷ֣��� ��ֵ��
��ֵ��