题目内容
如图,已知在平面直角坐标系xOy中,抛物线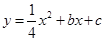 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求 的值;
的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45º,求点D的坐标.
(1)M(2,4);(2)tan∠MAC=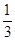 ;(3)
;(3)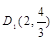 ,
,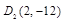 .
.
解析试题分析:
(1)根据与y轴的交点C的坐标(0,-3)就可以求出OC的值及c的值,进而求出OA的值及A的坐标,由待定系数法就可以求出b的值而求出解析式及定点坐标;
(2)如图1,过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.在Rt△AHM中,HM=AH=4,就可以求出AM的值,再由待定系数法求出直线AC的解析式,就可以求出点N的坐标,进而求出MN的值,由勾股定理就可以求出ME及NE的值,从而求出AE的值就可以得出结论;
(3)如图2,分类讨论,当D点在AC上方时,根据角之间的关系就可以求出∠D1AH=∠CAM,当D点在AC下方时,∠MAC=∠AD2M就可以求出点D的坐标. 试题解析:
试题解析:
∵C(0,-3),∴OC=3.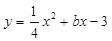
∵OA=2OC,∴OA=6.
∵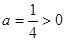 ,点A在点B右侧,抛物线与y轴交点C(0,-3)
,点A在点B右侧,抛物线与y轴交点C(0,-3)
∴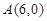 .
.
∴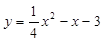 .
.
∴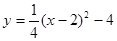 ,∴
,∴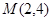 .
.
(2)过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.
在Rt△AHM中,HM=AH=4,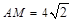 ,
,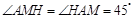 .求得直线AC的表达式为
.求得直线AC的表达式为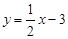 .
.
∴N(2,-2).∴MN=2.
在Rt△MNE中,∴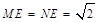 ,
,
∴ .
.
在Rt△AEN中, .
.
(3)?当D点在AC上方时,
∵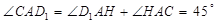 ,
,
又 ∵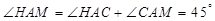 ,
,
∴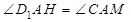 .
.
∴
∵点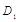 在抛物线的对称轴直线x=2上,
在抛物线的对称轴直线x=2上,
∴ ,∴
,∴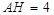 .
.
在Rt△AH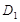 中,
中, .
.
∴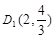 .
.
?当D点在AC下方时,
∵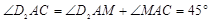 ,
,
又 ∵∠AMH=∠D2AM+∠AD2M=45º,
∴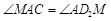 .
.
∴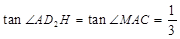
在Rt△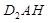 中,
中,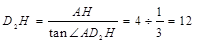 .
.
∴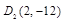 .
.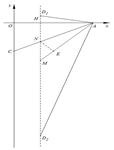
综上所述: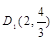 ,
,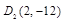 .
.
考点:二次函数综合题.

 与x轴的交点个数为
与x轴的交点个数为  箱与销售价
箱与销售价 元/箱之间的函数关系式.
元/箱之间的函数关系式.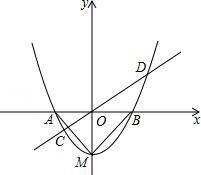

 中,
中, ,
, ,两动点
,两动点 分别在边
分别在边 上滑动,且
上滑动,且 ,以
,以 为边向下作正方形
为边向下作正方形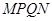 ,设其边长为
,设其边长为 ,正方形
,正方形 .
. 上高
上高 ;
;  时,
时, 恰好落在边
恰好落在边 关于
关于
 x2+
x2+ x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
 经过A
经过A 、C(0,4)两点,与x轴的另一交点是B.
、C(0,4)两点,与x轴的另一交点是B. 在第一象限的抛物线上,求点D关于直线BC的对称点
在第一象限的抛物线上,求点D关于直线BC的对称点 的坐标;
的坐标; 的图象经过点E,点
的图象经过点E,点 在此反比例函数图象上,求
在此反比例函数图象上,求 的值.
的值.