Question

如图甲，四边形OABC的边OA、OC分别在x轴、y轴的正半轴上，顶点在B点的抛物线交x轴于点A、D，交y轴于点E，连结AB、AE、BE．已知tan∠CBE=，A(3，0)，D(－1，0)，E(0，3)．
(1)求抛物线的解析式及顶点B的坐标；
(2)求证：CB是△ABE外接圆的切线；
(3)试探究坐标轴上是否存在一点P，使以D、E、P为顶点的三角形与△ABE相似，若存在，直接写出点P的坐标；若不存在，请说明理由；
(4)设△AOE沿x轴正方向平移t个单位长度(0＜t≤3)时，△AOE与△ABE重叠部分的面积为s，求s与t之间的函数关系式，并指出t的取值范围．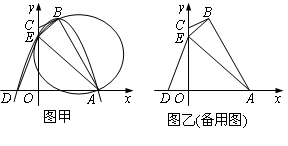

Answer 1

（1）y=－x²＋2x＋3．B(1，4)．（2）证明见解析；（3）P₁(0，0)，P₂(9，0)，P₃(0，－)．（4）s=.

解析试题分析：(1)利用两根式列出二次函数解析式y=a(x－3)(x＋1)，把将E(0，3)代入即可求出a的值，继而可求顶点B的坐标；
（2）过点B作BM⊥y于点M，利用已知条件先证明AB是△ABE外接圆的直径．再证CB⊥AB即可．
（3）存在；
（4）分两种情况进行讨论即可.
试题解析：(1)解：由题意，设抛物线解析式为y=a(x－3)(x＋1)．
将E(0，3)代入上式，解得：a=－1．
∴y=－x²＋2x＋3．
则点B(1，4)．
(2)如图，证明：过点B作BM⊥y于点M，则M(0，4)．
在Rt△AOE中，OA=OE=3，
∴∠1=∠2=45°，AE==3．
在Rt△EMB中，EM=OM－OE=1=BM，
∴∠MEB=∠MBE=45°，BE==．
∴∠BEA=180°－∠1－∠MEB=90°．
∴AB是△ABE外接圆的直径．
在Rt△ABE中，tan∠BAE===tan∠CBE，
∴∠BAE=∠CBE．
在Rt△ABE中，∠BAE＋∠3=90°，
∴∠CBE＋∠3=90°．
∴∠CBA=90°，即CB⊥AB．
∴CB是△ABE外接圆的切线．

(3)P₁(0，0)，P₂(9，0)，P₃(0，－)．
(4)解：设直线AB的解析式为y=kx＋b．
将A(3，0)，B(1，4)代入，得解得
∴y=－2x＋6．
过点E作射线EF∥x轴交AB于点F，当y=3时，得x=，
∴F(，3)．
情况一：如图7，当0＜t≤时，设△AOE平移到△DNM的位置，MD交AB于点H，MN交AE于点G．
则ON=AD=t，过点H作LK⊥x轴于点K，交EF于点L．
由△AHD∽△FHM，得．即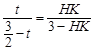．解得HK=2t．
∴S_阴=S_△MND－S_△GNA－S_△HAD=×3×3－(3－t)2－t·2t=－t2＋3t．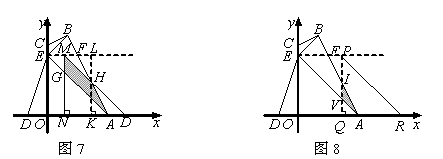

情况二：如图8，当＜t≤3时，设△AOE平移到△PQR的位置，PQ交AB于点I，交AE于点V．由△IQA∽△IPF，得．即．解得IQ=2(3－t)．
∴S阴=S△IQA－S△VQA=×(3－t)×2(3－t)－(3－t)2=(3－t)2=t2－3t＋．
综上所述：s=.
考点：二次函数综合题.