Question

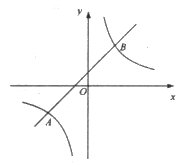
【题目】如图，在平面直角坐标系中，直线与直线交于点与轴交于点，点在轴上，过点作轴于点，交于点，交于.

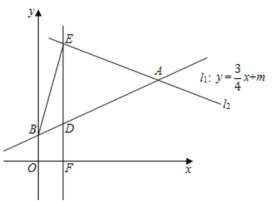
(1)求直线的解析式和点坐标.

(2)求①的面积与的关系式.并求出当的面积为时，点坐标.在轴上确定点，使得的面积等于面积，直接写出点的坐标；

②若直线将分成面积相等的两部分，求的值.

③若是直线上一点，点是直线上一点，使得当沿着折叠后与重合，请直接写出点和点的坐标.

Answer 1

【答案】（1）点B为（0，1），直线l1：y=x+1；直线l2：y=x+8；（2）①点M的坐标为：（0，）或（0，）；②k=；③点Q（0，1），点P为（1，1）．

【解析】

（1）l1与y轴交于点B，则点B（0，m），将点A、B的坐标代入l1：y=x+m并解得：m=1，故点A、B的坐标分别为：（4，4）、（0，1），即可求解；

（2）①设点M（0，t），△BMA的面积等于△BEA面积，则点M、E所在的直线与AB平行，即可求解；

②直线y=kx-k+7=k（x-1）+7，当x=1时，y=7，即直线过点（1，7），即过点E，设直线交AB于点R，直线y=kx-k+7将△BEA分成面积相等的两部分，则点R是AB的中点，坐标为：（2，），即可求解；

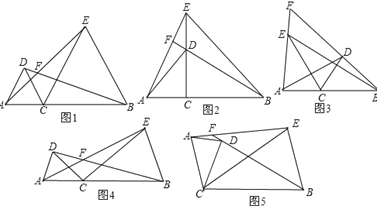
③如图2，AB=5，AF=5，故AB=AF，则当△PFA沿着AP折叠后与△QPA重合时，点Q与点B重合，即点Q（0，1），即可求解．

解：（1）l1与y轴交于点B，则点B（0，m），

将点A、B的坐标代入l1：y=x+m并解得：m=1，

∴点A、B的坐标分别为：（4，4）、（0，1），

将点A坐标代入l2表达式并解得：k=1，

∴直线l1：y=x+1；直线l2：y=x+8；

（2）设点F（a，0），则点D（a，a+1）、点E（a，-a+8），

△BEA的面积=×DE×xA=×（-a+8-a-1）×4=，

解得：a=1，

故点F、D、E的坐标分别为：（1，0）、（1，）、（1，7）；

①设点M（0，t），△BMA的面积等于△BEA面积，则点M、E所在的直线与AB平行，

当M在AB上方时，

由E、M的坐标的直线EM的表达式为：y=x+t，

将点E的坐标代入上式并解得：t=，

故点M（0，）；

当M（M′）在AB下方时，

则点M′、M关于点B对称，则点M′（0，），
故点M的坐标为：（0，）或（0，）；

②直线y=kx-k+7=k（x-1）+7，当x=1时，y=7，即直线过点（1，7），即过点E，

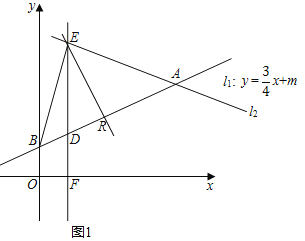
设直线交AB于点R，直线y=kx-k+7将△BEA分成面积相等的两部分，

则点R是AB的中点，坐标为：（2，）；

将点R的坐标代入y=kx-k+7，

∴，

解得：k=；

③如图2，AB=5，AF=5，故AB=AF，

则当△PFA沿着AP折叠后与△QPA重合时，点Q与点B重合，即点Q（0，1）

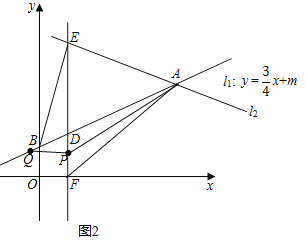
而OF=1，而PQ=PF，故PF=1，

故点P为（1，1）．