题目内容
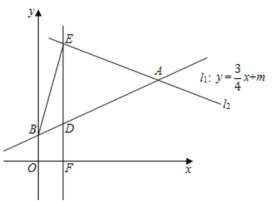
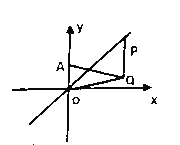
【题目】已知点![]() 是直线
是直线![]() 上一动点,点
上一动点,点![]() 在点
在点![]() 的下方,且
的下方,且![]() 轴,
轴,![]() 轴上有一点
轴上有一点![]() ,当
,当![]() 值最小时,点
值最小时,点![]() 的坐标为___________.
的坐标为___________.
【答案】(![]() ,
,![]() )
)
【解析】
过点Q作y=x的平行线,求出该直线的解析式为y=x![]() 4,作O关于该平行线的对称点O',连接AO',AO'与y=x
4,作O关于该平行线的对称点O',连接AO',AO'与y=x![]() 4的交点为Q点,则AO'即为AQ+OQ的最小长;求出O'(4,
4的交点为Q点,则AO'即为AQ+OQ的最小长;求出O'(4,![]() 4),AO'的直线解析式y=
4),AO'的直线解析式y=![]() ,Q点为y=
,Q点为y=![]() 与y=x
与y=x![]() 4的交点,联立求解即可.
4的交点,联立求解即可.
解:过点Q作y=x的平行线,
∵PQ=4,
∴平行线的解析式为:y=x![]() 4,
4,
作O关于该平行线的对称点O',连接AO',
∴点![]() 的坐标为(4,
的坐标为(4,![]() ),
),![]() ,
,
AO'与y=x![]() 4的交点为Q点,
4的交点为Q点,
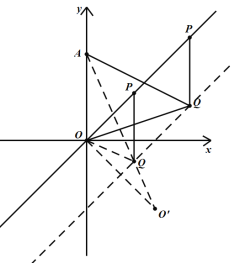
∴AO'即为AQ+OQ的最小长;
∵O'(4,![]() 4),
4),
∵A(0,5),
设![]() 为
为![]() ,
,
∴![]() ,解得:
,解得: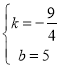 ,
,
∴AO'的直线解析式为:y=![]() ,
,
∴Q点为y=![]() 与y=x
与y=x![]() 4的交点,
4的交点,
∴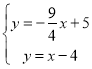 ,解得:
,解得: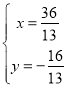 ,
,
∴Q(![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目