题目内容
1.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( )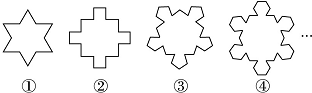
| A. | n(n-1) | B. | n(n+1) | C. | (n+1)(n-1) | D. | n2+2 |
分析 由题意可知:等边三角形“扩展”而来的多边形的边数为12=3×(3+1),正方形“扩展”而来的多边形的边数为20=4×(4+1),正五边形“扩展”而来的多边形的边数为30=5×(5+1),正六边形“扩展”而来的多边形的边数为42=6×(6+1),…所以正n边形“扩展”而来的多边形的边数为n(n+1),据此解答即可.
解答 解:∵等边三角形“扩展”而来的多边形的边数为:
12=3×(3+1),
正方形“扩展”而来的多边形的边数为:
20=4×(4+1),
正五边形“扩展”而来的多边形的边数为:
30=5×(5+1),
正六边形“扩展”而来的多边形的边数为:
42=6×(6+1),
…
∴正n边形“扩展”而来的多边形的边数为:n(n+1).
故选:B.
点评 题主要考查了图形的变化规律,注意观察总结出规律,并能正确应用,解答此题的关键是判断出正n边形“扩展”而来的多边形的边数与n的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
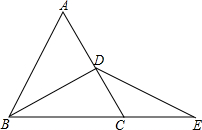 已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.
已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.
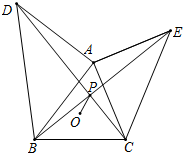 如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$.
如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是5-$\frac{5}{3}\sqrt{3}$.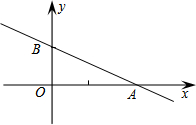 如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.
如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.