题目内容
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;

小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC=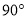 ,
,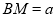 ,
, (其中
(其中 ),直接写出AM的长(用含有a,b的代数式表示).
),直接写出AM的长(用含有a,b的代数式表示).
(1)【解析】
延长MB至点E,使BE=MC,连接AE,
∵△ABC是等边三角形,
∴AB=AC,
∵四边形ABMC是⊙O的内接四边形,
∴∠ABE=∠ACM,

在△AEB和△AMC中 ,∴△AEB≌△AMC,
,∴△AEB≌△AMC,
∴∠AEB=∠AMC,
∵∠AMC=∠ABC(在同圆中,同弧所对的圆周角相等),
∴∠AEB=∠ABC,
∵∠AME=∠ACB(在同圆中,同弧所对的圆周角相等),
又∵∠ABC=∠ACB=60°,
∴∠AEB=∠AME=60°,
∴△AEM是等边三角形,
∴AM=ME=MB+BE,
∵BE=MC,
∴MB+MC=MA=1+2=3.
即AM的长是3.
(2)【解析】
分为两种情况:①如图,AM= =
= (a+b)
(a+b)

由是:延长MB至点E,使BE=MC,连AE,
由(1)知:∠ABE=∠ACM,
在△ABE和△ACM中
∴△ABE≌△ACM,
∴AM=AE,∠E=∠AMC,
∵∠AMC=∠ABC=45°,∠AMB=∠ACB=45°,
∴∠E=∠AMB=45°,
∴∠EAM=90°,
在△EAM中,ME=MB+BE=MB+CM=a+b,AE=AM,
由勾股定理得:AM= =
= (a+b)
(a+b)
即AM= (a+b)
(a+b)
②如图,

在CM上截取CN=BM,连接AN,
∵∠ABM所对的弧和∠ACN所对的弧都是弧AM,
∴∠ABM=∠ACN,
在△ABM和△ACN中
∴△ABM≌△ACN(SAS),
∴AM=AN,∠BAM=∠CAN,
∵∠BAC=∠BAN+∠CAN=90°,
∴∠BAN+∠BAM=90°,
∴∠MAN=90°,
则△MAN是等腰直角三角形,
∵MN=CM-CN=CM-BM=b-a,
由勾股定理得:AM=AN= =
= (b-a)
(b-a)
即AM= (b-a).
(b-a).
即AM的长是 (a+b)或
(a+b)或 (b-a).
(b-a).
【解析】
试题分析:(1)延长MB至点E,使BE=MC,连AE,根据等边三角形性质求出AC=AB,根据圆内接
四边形的性质推出∠ABE=∠ACM,证△ABE≌△ACM,推出AM=AE,证等边三角形AEM,推出AE=AM=ME,
即可推出答案;
(2)分为两种情况,画出图形,延长MB至点E,使BE=MC,连AE,根据等腰直角三角形性质推
出AB=AC,根据SAS证△ABE≌△ACM,推出AM=AE,∠E=∠AMC=45°,∠AMB=45°,求出△EAM是
等腰直角三角形,根据勾股定理求出即可.
考点:圆周角定理,全等三角形的判定与性质,等边三角形的判定,勾股定理,等腰直角三角形,
圆内接四边形的性质,三角形的外接圆与内心。




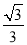 x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).

