题目内容
7.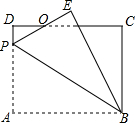 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.
分析 由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
解答 解:如图所示: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
$\left\{\begin{array}{l}{∠D=∠E}&{\;}\\{OD=OE}&{\;}\\{∠DOP=∠EOG}&{\;}\end{array}\right.$,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
故答案为:4.8.
点评 本题考查了矩形的性质、折叠的性质、全等三角形的判定与性质、勾股定理;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
17.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
| A. | 众数是35 | B. | 中位数是34 | C. | 平均数是35 | D. | 方差是6 |
15.为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍?
19.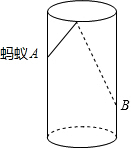 如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
 如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )
如图,透明的圆柱形容器(容器厚度忽略 不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是( )| A. | 13cm | B. | 2$\sqrt{61}$cm | C. | $\sqrt{61}$cm | D. | 2$\sqrt{34}$cm |
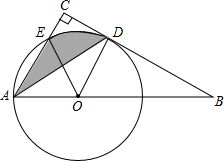 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD. 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.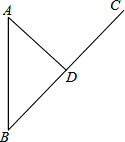 如图,某沿海城市A接到台风警报,在该市正南方向$120\sqrt{2}$km有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15km/h的速度向C移动,AD⊥BC于D,如果在距台风中心150km的区域内都将受到台风的影响,请问:
如图,某沿海城市A接到台风警报,在该市正南方向$120\sqrt{2}$km有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15km/h的速度向C移动,AD⊥BC于D,如果在距台风中心150km的区域内都将受到台风的影响,请问: