题目内容
10.若2a=3,2b=5,2c=75,试说明:a+2b=c.分析 首先根据幂的乘方的运算方法,求出(2b)2=25,然后根据同底数幂的乘法法则,判断出2a+2b=2c,即可判断出a+2b=c.
解答 证明:∵2b=5,
∴(2b)2=25,
即22b=25,
又∵2a=3,
∴2a×22b=3×25=75,
∴2a+2b=2c,
∴a+2b=c.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.

练习册系列答案
相关题目
6.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | (-a2b)3=-a6b3 | C. | a2•a3=a6 | D. | a8÷a2=a4 |
19.下列计算正确的是( )
| A. | $\sqrt{13}+\sqrt{3}=\sqrt{16}=4$ | B. | $\sqrt{121÷4}=\sqrt{121}÷\sqrt{4}=\frac{11}{2}$ | C. | $3+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{4\frac{1}{3}}=2\sqrt{\frac{1}{3}}$ |
20.下列说法中,正确的是( )
| A. | 打开电视机,正在播广告,是必然事件 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% | |
| D. | 从一个只装有白球的缸里摸出一个球,摸出的球是白球 |
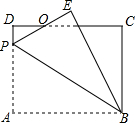 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为4.8. 北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
北京时间2015年04月25日14时11分,尼泊尔发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)