题目内容
(本小题10分)如图,已知在△ABC中,AD是∠BAC平分线,点E在AC边上,且∠AED=∠ADB.

求证:(1)△ABD∽△ADE;(2)AD2=AB·AE.
(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)因为如果两个三角形的两个对应角相等,那么这两个三角形相似,∠BAD=∠DAE,∠AED=∠ADB,可得证△ABD∽△ADE;
(2)又因为相似三角形的对应边成比例可得:AD:AE=AB:AD,变形即可证得.
试题解析:(1)∵AD是内角平分线,∴∠BAD=∠DAE,∵∠AED=∠ADB,∴△ABD∽△ADE;
(2)∵△ABD∽△ADE,∴AD:AE=AB:AD,∴AD2=ABAE.
考点:相似三角形的判定与性质.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,其中
,其中 .
. 等于( )
等于( )
 B.
B. C.
C. D.
D.
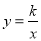 (
(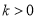 )交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是
)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是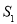 ,△BOD面积是
,△BOD面积是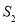 ,△POE面积是
,△POE面积是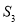 ,则( )
,则( )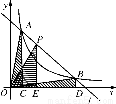
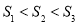 B.
B.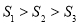 C.
C. D.
D.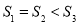

 -3x+4=0的根的情况是( )
-3x+4=0的根的情况是( )