题目内容
13.Rt△ABC中,∠ACB=90°,AC=6,BC=8,则它的内切圆半径是2.分析 ⊙O切AC于E,切BC于F,切AB于G,连OE,OF,根据切线的性质得到OE⊥AC,OF⊥BC,则四边形CEOF为正方形,得到CE=CF=r,根据切线长定理得AE=AG=6-r,BF=BG=8-r,利用6-r+8-r=10可求出r.
解答 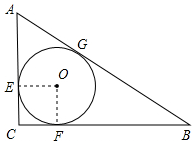 解:如图,⊙O切AC于E,切BC于F,切AB于G,连OE,OF,
解:如图,⊙O切AC于E,切BC于F,切AB于G,连OE,OF,
∴OE⊥AC,OF⊥BC,
∴四边形CEOF为正方形,
∵∠C=90°,AC=6,BC=8,
∴AB=10,
设⊙O的半径为r,则CE=CF=r,
∴AE=AG=6-r,BF=BG=8-r,
∴AB=AG+BG=AE+BF,即6-r+8-r=10,
∴r=2.
故答案为2.
点评 本题考查了圆的切线的性质和切线长定理:圆的切线垂直于过切点的半径;从圆外一点引圆的两条切线,切线长相等.

练习册系列答案
相关题目
10.有理数-$\frac{1}{5}$的倒数为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | $-\frac{1}{5}$ | D. | -5 |
4.若代数式$\frac{2}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x≠2 | C. | x>2 | D. | x=2 |
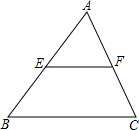 如图,EF为△ABC的中位线,△AEF的面积为6,则四边形EBCF的面积为18.
如图,EF为△ABC的中位线,△AEF的面积为6,则四边形EBCF的面积为18. 如图,已知圆锥的底面半径OB为1,高所在直线AO与母线AB的夹角为30°.圆锥的侧面积为2π.
如图,已知圆锥的底面半径OB为1,高所在直线AO与母线AB的夹角为30°.圆锥的侧面积为2π.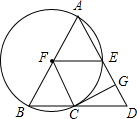 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.