题目内容
4. 如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( )
如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( )| A. | (5,3) | B. | (5,4) | C. | (3,5) | D. | (4,5) |
分析 过P作PC⊥AB于点C,过P作PD⊥x轴于点D,由切线的性质可求得PD的长,则可得PB的长,由垂径定理可求得CB的长,在Rt△PBC中,由勾股定理可求得PC的长,从而可求得P点坐标.
解答 解: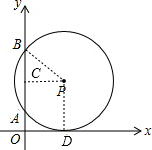
如图,过P作PC⊥AB于点C,过P作PD⊥x轴于点D,连接PB,
∵P为圆心,
∴AC=BC,
∵A(0,2),B(0,8),
∴AB=8-2=6,
∴AC=BC=3,
∴OC=8-3=5,
∵⊙P与x轴相切,
∴PD=PB=OC=5,
在Rt△PBC中,由勾股定理可得PC=$\sqrt{P{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴P点坐标为(4,5),
故选D.
点评 本题主要考查切线的性质和垂径定理,利用切线的性质求得圆的半径是解题的关键.

练习册系列答案
相关题目
14.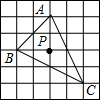 △ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
 △ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )| A. | 三条垂直平分线的交点 | B. | 三条内角角平分线的交点 | ||
| C. | 重心 | D. | 无法确定 |
19.下列方程是一元一次方程的是( )
| A. | x2+1=0 | B. | (x+2)2-1=3 | C. | 3x+2=5-x | D. | x+y=3 |
16.下列各数中互为相反数的有( )
| A. | +(-5.2)与-5.2 | B. | +(+5.2)与-5.2 | C. | -(-5.2)与5.2 | D. | 5.2与+|-5.2| |
6. 如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )
如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )
 如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )
如图,在△ABC中,DE∥BC交AB于点D,交AC于点E.若AB=4,AC=3,AD=3,则AE的长为( )| A. | $\frac{4}{9}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{9}{4}$ |
 如图,|a-b|-$\sqrt{{b}^{2}}$=a.
如图,|a-b|-$\sqrt{{b}^{2}}$=a. 作图题
作图题 如图,在△ABC中,AB=AC,∠BAC=108°,BD=DC,则∠BAD的度数为54°.
如图,在△ABC中,AB=AC,∠BAC=108°,BD=DC,则∠BAD的度数为54°.