题目内容
 四边形ABCD的顶点坐标分别为(-1,4)、(-4,3)、(-5,0),(4,0).
四边形ABCD的顶点坐标分别为(-1,4)、(-4,3)、(-5,0),(4,0).(1)在如图的平面直角坐标系中描出这四个点;
(2)计算这个四边形的面积;
(3)如果把原来ABCD各顶点的纵坐标保持不变,横坐标增加2,得到四边形A′B′C′D′,请直接写出四边形A′B′C′D′面积.
考点:作图-平移变换
专题:
分析:(1)利用已知点的坐标在坐标系中描出即可;
(2)将已知三边形分割,利用S=S△BCE+S四边形BEFA+S△AFD求出即可;
(3)利用平移的性质得出四边形A′B′C′D′面积.
(2)将已知三边形分割,利用S=S△BCE+S四边形BEFA+S△AFD求出即可;
(3)利用平移的性质得出四边形A′B′C′D′面积.
解答: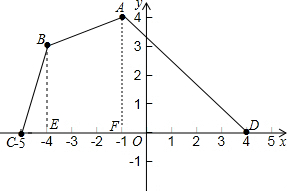 解:(1)如图所示:
解:(1)如图所示:
(2)S=S△BCE+S四边形BEFA+S△AFD
=
×1×3+
(3+4)×3+
×5×4
=22;
(3)由题意可得:把原来ABCD各顶点的纵坐标保持不变,横坐标增加2,得到四边形A′B′C′D′,相当于四边形ABCD向上平移2个单位,故四边形A′B′C′D′面积不变为:22.
 解:(1)如图所示:
解:(1)如图所示:(2)S=S△BCE+S四边形BEFA+S△AFD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=22;
(3)由题意可得:把原来ABCD各顶点的纵坐标保持不变,横坐标增加2,得到四边形A′B′C′D′,相当于四边形ABCD向上平移2个单位,故四边形A′B′C′D′面积不变为:22.
点评:此题主要考查了平移的性质以及四边形面积求法,正确分割四边形是解题关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
在下列多项式的乘法中,不能用平方差公式计算的是( )
| A、(-m-n)(-m+n) |
| B、(x3-y3)(x3-y3) |
| C、(-a-b)(a-b) |
| D、(c2-d2)(d2+c2) |
 在△ABC中,∠A=90°,CD平分∠ACB,DE⊥BC于点E,若AB=6,则DE+DB=( )
在△ABC中,∠A=90°,CD平分∠ACB,DE⊥BC于点E,若AB=6,则DE+DB=( )| A、4 | B、5 | C、6 | D、7 |
 如图,矩形ABOC的面积为6,若反比例函数y=
如图,矩形ABOC的面积为6,若反比例函数y=| k |
| x |
| A、3 | B、-3 | C、6 | D、-6 |
下列说法正确的是( )
| A、单项式a的次数是0 | ||
| B、a的系数为0 | ||
| C、-9是单项式 | ||
D、
|
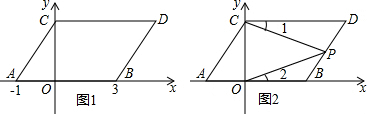
 如图,△AOC旋转后能与△BOD重合,则△AOC与
如图,△AOC旋转后能与△BOD重合,则△AOC与