题目内容
如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(温馨提示:由平移性质可知:AB∥CD.)
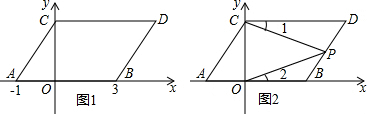
(1)求点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABCD?若存在这样的点,求出点P的坐标;若不存在,试说明理由.
(3)如图2,点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合),
的值是否变化?若变化,请说明理由;若不变,求出这个值.

(1)求点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABCD?若存在这样的点,求出点P的坐标;若不存在,试说明理由.
(3)如图2,点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合),
| ∠1+∠2 |
| ∠CPO |
考点:坐标与图形性质,三角形的面积,三角形内角和定理,三角形的外角性质,坐标与图形变化-平移
专题:计算题
分析:(1)根据点的平移规律得到C点和D点坐标,然后根据平行四边形的面积公式计算四边形ABDC的面积.
(2)设P点坐标为(0,t),根据三角形面积公式得到
•4•|t|=8,解得t=±4,然后写出P点坐标;
(3)作PQ∥CD,如图2,由CD∥AB得到PQ∥AB,则根据平行线的性质得∠1=∠3,∠2=∠4,所以∠1+∠2=∠3+∠4=∠CPO,易得
=1.
(2)设P点坐标为(0,t),根据三角形面积公式得到
| 1 |
| 2 |
(3)作PQ∥CD,如图2,由CD∥AB得到PQ∥AB,则根据平行线的性质得∠1=∠3,∠2=∠4,所以∠1+∠2=∠3+∠4=∠CPO,易得
| ∠1+∠2 |
| ∠CPO |
解答: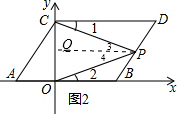 解:(1)点C的坐标为((0,2),D点坐标为(4,2),
解:(1)点C的坐标为((0,2),D点坐标为(4,2),
∵AC∥BD,
∴四边形ABCD为平行四边形,
∴四边形ABDC的面积=2×4=8;
(2)存在.
设P点坐标为(0,t),
∵S△PAB=S四边形ABCD,
∴
•4•|t|=8,解得t=±4,
∴P点坐标为(0,4)或(0,-4);
(3)不变化.
作PQ∥CD,如图2,
∵CD∥AB,
∴PQ∥AB,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠CPO,
∴
=1.
 解:(1)点C的坐标为((0,2),D点坐标为(4,2),
解:(1)点C的坐标为((0,2),D点坐标为(4,2),∵AC∥BD,
∴四边形ABCD为平行四边形,
∴四边形ABDC的面积=2×4=8;
(2)存在.
设P点坐标为(0,t),
∵S△PAB=S四边形ABCD,
∴
| 1 |
| 2 |
∴P点坐标为(0,4)或(0,-4);
(3)不变化.
作PQ∥CD,如图2,
∵CD∥AB,
∴PQ∥AB,
∴∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=∠CPO,
∴
| ∠1+∠2 |
| ∠CPO |
点评:本题考查了坐标与图形性质:利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系.也考查了平移的性质和平行线的性质.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在下列各数中是无理数的有( )
-0.333…,
,
,3π,3.141 5,2.010 101…(相邻两个1之间有1个0).
-0.333…,
| 4 |
| 5 |
| A、2个 | B、3个 | C、4个 | D、5个 |
在下列各数0.05,-
,0,2014,
中,有理数有( )
| 2 |
| 3 |
| 22 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列各数中负数是( )
| A、1 | B、0 |
| C、-2013 | D、2014 |
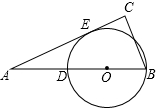 如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径.
如图,在Rt△ABC中,∠C=90°,D是AB上的一点,以BD为直径的⊙O切AC于点E,AE=4,AD=2,求⊙O半径.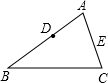 如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长.
如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长. 四边形ABCD的顶点坐标分别为(-1,4)、(-4,3)、(-5,0),(4,0).
四边形ABCD的顶点坐标分别为(-1,4)、(-4,3)、(-5,0),(4,0).