题目内容
在△ABC中,BD、CF分别是AC、AB边上的中线,且BD=CF,则△ABC是( )
| A、不等边三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、直角三角形 |
考点:全等三角形的判定与性质,平行四边形的判定与性质
专题:
分析:根据三角形的中位线定理可得DF∥BC,过D作DE∥CF.即可得出四边形DFCE是平行四边形由平行四边形的性质得出∠1=∠E=∠2,从而可得△DBC≌△FCB,则∠DCB=∠FBC,则AB=AC.
解答: 解:∵DF分别为AC、AB的中点,
解:∵DF分别为AC、AB的中点,
∴DF∥BC,
过D作DE∥CF交BC的延长线于E.
∴四边形DFCE是平行四边形,
∴DE=CF,
∵BD=CF,
∴DB=DE,
∴∠1=∠E=∠2,
从而可得△DBC≌△FCB,
∴∠DCB=∠FBC,
∴AB=AC.
故选B.
 解:∵DF分别为AC、AB的中点,
解:∵DF分别为AC、AB的中点,∴DF∥BC,
过D作DE∥CF交BC的延长线于E.
∴四边形DFCE是平行四边形,
∴DE=CF,
∵BD=CF,
∴DB=DE,
∴∠1=∠E=∠2,
从而可得△DBC≌△FCB,
∴∠DCB=∠FBC,
∴AB=AC.
故选B.
点评:本题考查了全等三角形的判定和性质以及平行四边形的判定和性质,根据等角对等边可证明三角形是等腰三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
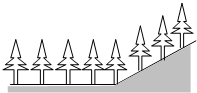 如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为3m.如果在坡度为1:3的山坡上种植树,也要求株距为3m,那么相邻两树
如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为3m.如果在坡度为1:3的山坡上种植树,也要求株距为3m,那么相邻两树间的坡面距离约为( )
| A、4m | B、3m |
| C、5.1m | D、3.2m |
在日历上,如果某月的11日是星期四,那么这个月里下面哪个日期是星期五?( )
| A、4日 | B、19日 |
| C、20日 | D、30日 |
若xn=2,yn=3,则(xy)3n等于( )
| A、12 | B、16 | C、18 | D、216 |
 如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为
如图,水坝横断面是梯形ABCD,坝顶宽为3m,坝高4m,斜坡AB长5m,斜坡CD的坡度i=1:1.则坝底AD长为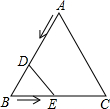 已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问:
已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问: