题目内容
3.已知x=$\frac{1}{1+\sqrt{2}}$,则$\sqrt{{x}^{3}+2{x}^{2}-x+8}$=2$\sqrt{2}$.分析 将x分母有理化,然后将x的值代入原式即可.
解答 解:由题意可知:x=$\frac{1-\sqrt{2}}{(1+\sqrt{2})(1-\sqrt{2})}$=$\sqrt{2}$-1,
∴x3+2x2-x+8
=x(x2+2x-1)+8
=x(x2+2x+1-2)+8
=x(x+1)2-2x+8
=($\sqrt{2}$-1)($\sqrt{2}$)2-2($\sqrt{2}$-1)+8
=2($\sqrt{2}$-1)-2($\sqrt{2}$-1)+8
=8,
∴原式=$\sqrt{8}$=2$\sqrt{2}$;
点评 本题考查二次根式的运算,涉及分母有理化,因式分解,二次根式运算等知识,属于中等题型.

练习册系列答案
相关题目
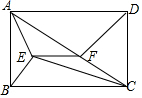 如图,ABCD是长方形,EF与BC平行,四边形AECF的面积是35,三角形AFD的面积是40,三角形BCE的面积是30,三角形CDF的面积是25,三角形ABE的面积是10.
如图,ABCD是长方形,EF与BC平行,四边形AECF的面积是35,三角形AFD的面积是40,三角形BCE的面积是30,三角形CDF的面积是25,三角形ABE的面积是10. 如图,已知AB2=AD×AC,S△ABD=2S△DBC,则AB:AC=$\sqrt{5}$:3.
如图,已知AB2=AD×AC,S△ABD=2S△DBC,则AB:AC=$\sqrt{5}$:3.