题目内容
4.如图,点M,A,H重合,点C在射线NA上,连接BC交圆O于点D,若点D为BC的中点.(1)求证:BN=CN;
(2)过点N作圆O的切线交BC的延长线于点K,若CK=CD,AB=2$\sqrt{6}$,求KN的长.
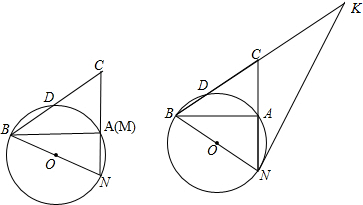
分析 (1)如图1所示,连接ND.首先证明∠BDN=90°,从而可得到DN是BC的垂直平分线;
(2)如图2所示,过点C作CM⊥BN,垂足为M.首先证明△CMN≌△BAN,从而得到CM=AB=2$\sqrt{6}$,然后再证明△BCM∽△BKN,由相似三角形的性质可求得KN的长.
解答 解:(1)如图1所示,连接ND.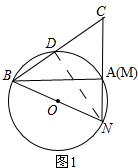
∵BN是圆O的直径,
∴∠BDN=90°.
∴DN⊥BC.
∵D是BC的中点,
∴DN是BC的垂直平分线.
∴BN=CN.
(2)如图2所示,过点C作CM⊥BN,垂足为M.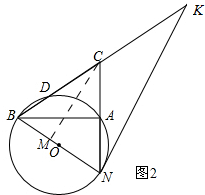
∵BN为圆O的直径,
∴∠BAN=90°.
∵CM⊥BN,
∴∠CMN=90°.
∴∠CMN=∠BAN.
在△CMN和△BAN中,
$\left\{\begin{array}{l}{∠CMN=∠BAN}\\{∠BNA=∠MNC}\\{BN=CN}\end{array}\right.$,
∴△CMN≌△BAN.
∴CM=AB=2$\sqrt{6}$.
∵NK是圆O的切线,
∴ON⊥NK.
∴CM∥KN.
∴△BCM∽△BKN.
∴$\frac{CM}{NK}=\frac{BC}{BK}=\frac{2}{3}$,即$\frac{2\sqrt{6}}{NK}=\frac{2}{3}$.
∴NK=3$\sqrt{6}$.
点评 本题主要考查的是切线的性质、相似三角形的性质和判定、线段垂直平分线的性质、全等三角形的性质和判定,掌握本题辅助线的作法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.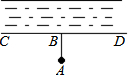 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )| A. | 两点之间线段最短 | B. | 点到直线的距离 | ||
| C. | 两点确定一条直线 | D. | 垂线段最短 |
16.计算:(-1)100+(-1)101的结果是( )
| A. | 1100 | B. | -1 | C. | 0 | D. | -1100 |
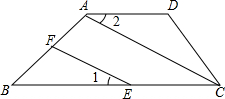 已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.
已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠1=∠2.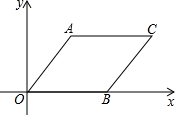 如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).
如图,在平面直角坐标系中,四边形AOBC是菱形.若点A的坐标是(3,4),则菱形的周长为20,点B的坐标是(5,0).