题目内容
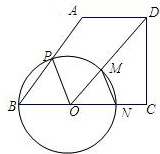 如图:已知,四边形ABCD中,AD∥BC,DC⊥BC,已知AB=5,BC=6,cosB=
如图:已知,四边形ABCD中,AD∥BC,DC⊥BC,已知AB=5,BC=6,cosB=| 3 | 5 |
(1)当BO=AD时,求BP的长;
(2)点O运动的过程中,是否存在BP=MN的情况?若存在,请求出当BO为多长时BP=MN;若不存在,请说明由;
(3)在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围.
分析:(1)过点A作AE⊥BC,在⊙O中,过点O作OH⊥AB,则四边形ADCE是矩形,可由余弦的概念,求得AE,则有AD=CE=BC-BE,而得到BO=AD的值,由垂径定理知,PH=BH,由BH:OB=cosB,求得BH,即有PB=2BH;
(2)用反证法,证明不存在BP=MN;
(3)由题意知,当点N在BC上时,⊙C与⊙O外切,有
<CN<6=BC,当点N在BC的延长线上时,⊙C与⊙O内切,由于点这在AB上,BP的最大值为5,则可利用余弦的概念,求得圆O的直径为
,故0<CN≤
-6=
.
(2)用反证法,证明不存在BP=MN;
(3)由题意知,当点N在BC上时,⊙C与⊙O外切,有
| 7 |
| 3 |
| 25 |
| 3 |
| 25 |
| 3 |
| 7 |
| 3 |
解答: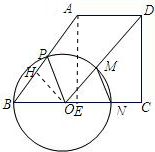 解:(1)过点A作AE⊥BC
解:(1)过点A作AE⊥BC
在Rt△ABE中,由AB=5,cosB=
,得BE=3
∵CD⊥BC,AD∥BC,BC=6
∴AD=EC=BC-BE=3
当BO=AD=3时,在⊙O中,过点O作OH⊥AB,则BH=HP,
∵
=cosB
∴BH=3×
=
∴BP=
(2)不存在BP=MN的情况.
假设BP=MN成立,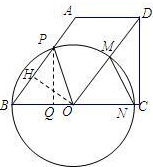
因为BP和MN为⊙O的弦,则必有∠BOP=∠DOC,
过P作PQ⊥BC,过点O作OH⊥AB,
∵CD⊥BC,则有△PQO∽△DCO
设BO=x,则PO=x,OC=6-x,
由
=cosB=
,得BH=
x,
∴BP=2BH=
x
∴BQ=BP×cosB=
x,PQ=
x
∴OQ=x-
x=
x
∵△PQO∽△DCO
∴
=
,即
=
得x=
当x=
时,BP=
x=
>5,与点P应在边AB上不符,
∴不存在BP=MN的情况.
(3)情况一:⊙O与⊙C相外切,此时0<CN<6;
情况二:⊙O与⊙C相内切,此时0<CN≤
.
 解:(1)过点A作AE⊥BC
解:(1)过点A作AE⊥BC在Rt△ABE中,由AB=5,cosB=
| 3 |
| 5 |
∵CD⊥BC,AD∥BC,BC=6
∴AD=EC=BC-BE=3
当BO=AD=3时,在⊙O中,过点O作OH⊥AB,则BH=HP,
∵
| BH |
| BO |
∴BH=3×
| 3 |
| 5 |
| 9 |
| 5 |
∴BP=
| 18 |
| 5 |
(2)不存在BP=MN的情况.
假设BP=MN成立,

因为BP和MN为⊙O的弦,则必有∠BOP=∠DOC,
过P作PQ⊥BC,过点O作OH⊥AB,
∵CD⊥BC,则有△PQO∽△DCO
设BO=x,则PO=x,OC=6-x,
由
| BH |
| x |
| 3 |
| 5 |
| 3 |
| 5 |
∴BP=2BH=
| 6 |
| 5 |
∴BQ=BP×cosB=
| 18 |
| 25 |
| 24 |
| 25 |
∴OQ=x-
| 18 |
| 25 |
| 7 |
| 25 |
∵△PQO∽△DCO
∴
| PQ |
| OQ |
| DC |
| OC |
| ||
|
| 4 |
| 6-x |
得x=
| 29 |
| 6 |
当x=
| 29 |
| 6 |
| 6 |
| 5 |
| 29 |
| 5 |
∴不存在BP=MN的情况.
(3)情况一:⊙O与⊙C相外切,此时0<CN<6;
情况二:⊙O与⊙C相内切,此时0<CN≤
| 7 |
| 3 |
点评:本题利用了余弦的概念、矩形的性质、垂径定理、直角三角形的性质、相似三角形的判定和性质、圆与圆的位置关系求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
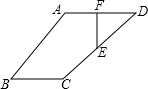 如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:
如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1: 如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式.
如图,已知平行四边形ABOC的顶点A、B、C在二次函数y=ax2+bx+c的图象上,又点A、B分别在y轴和x轴上,∠ABO=45°.图象顶点的横坐标为2,求二次函数解析式. 如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.
如图,已知:四边形ABCD中,AD=BC,E、F分别是DC、AB的中点,直线EF分别与BC、AD的延长线相交于G、H.求证:∠AHF=∠BGF.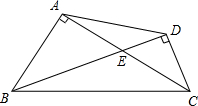 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,
如图,已知平行四边形ABCD,点E是AD边上的点,且AE=2ED,连接BE并延长交CD的延长线于点F,