题目内容
18.若最简根式$\root{3a-b}{4a+3b}$与根式$\sqrt{2a{b^2}-{b^3}+6{b^2}}$是同类二次根式,求a+b=2.分析 利用同类二次根式定义列出方程组,求出方程组的解得到a与b的值,即可求出a+b的值.
解答 解:化简得:$\sqrt{2a{b^2}-{b^3}+6{b^2}}$=|b|$\sqrt{2a-b+6}$,
由题意得:$\left\{\begin{array}{l}{3a-b=2}\\{4a+3b=2a-b+6}\end{array}\right.$,即$\left\{\begin{array}{l}{3a-b=2①}\\{a+2b=3②}\end{array}\right.$,
①×2+②得:7a=7,即a=1,
把a=1代入②得:b=1,
则a+b=2,
故答案为:2
点评 此题考查了同类二次根式,熟练掌握同类二次根式的定义是解本题的关键.

练习册系列答案
相关题目
6.方程x2=2x的解是( )
| A. | x1=-2,x2=0 | B. | x1=$\sqrt{2}$,x2=0 | C. | x1=1,x2=2 | D. | x1=2,x2=0 |
7.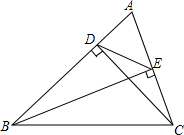 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )| A. | AE=3 | B. | BE=$\frac{1}{3}$$\sqrt{713}$ | C. | CE=$\frac{14}{3}$ | D. | DE=2 |
8.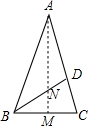 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
 如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )| A. | ∠BAC=36° | |
| B. | BD平分∠ABC | |
| C. | 若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54° | |
| D. | 点N是BD的中点 |
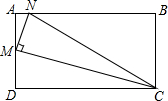 在如图所示的矩形ABCD中,已知MN丄MC,且M为AD的中点,AN=2,tan∠MCN=$\frac{1}{4}$,则AB等于( )
在如图所示的矩形ABCD中,已知MN丄MC,且M为AD的中点,AN=2,tan∠MCN=$\frac{1}{4}$,则AB等于( )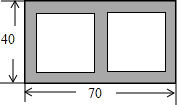 如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的$\frac{1}{8}$,则路宽x应满足的方程是(70-3x)(40-2x)=40×70×(1-$\frac{1}{8}$).
如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的$\frac{1}{8}$,则路宽x应满足的方程是(70-3x)(40-2x)=40×70×(1-$\frac{1}{8}$).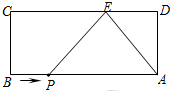 如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.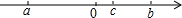 有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.
有理数a、b、c在数轴上的位置如图所示,则|a-b|-|2a-c|=a+b-c.