题目内容
8.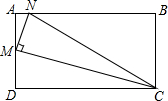 在如图所示的矩形ABCD中,已知MN丄MC,且M为AD的中点,AN=2,tan∠MCN=$\frac{1}{4}$,则AB等于( )
在如图所示的矩形ABCD中,已知MN丄MC,且M为AD的中点,AN=2,tan∠MCN=$\frac{1}{4}$,则AB等于( )| A. | 32 | B. | 28 | C. | 36 | D. | 40 |
分析 通过证得△AMN∽△DCM,对应边成比例即可求得.
解答 解:∵MN丄MC,tan∠MCN=$\frac{1}{4}$,
∴$\frac{MN}{MC}$=$\frac{1}{4}$,
∵∠AMN+∠DMC=90°,∠AMN+∠ANM=90°,
∴∠ANM=∠DMC,
∵∠A=∠D=90°,
∴△AMN∽△DCM,
∴$\frac{AN}{DM}$=$\frac{MN}{MC}$=$\frac{1}{4}$,
∵AN=2,
∴MD=8,
∵M为AD的中点,
∴AM=8,
∵△AMN∽△DCM,
∴$\frac{AM}{DC}$=$\frac{MN}{CM}$=$\frac{1}{4}$,
∴$\frac{8}{DC}$=$\frac{1}{4}$,
∴DC=32,
∴AB=32.
故选A.
点评 本题考查了矩形的性质,三角形相似的判定和性质以及解直角三角形等,证得三角形相似是解题的关键.

练习册系列答案
相关题目
13.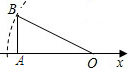 如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
 如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -2 | D. | -$\sqrt{3}$ |
20.点P(-5,5)在平面直角坐标系中所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
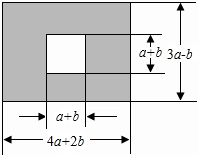 眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.