题目内容
19.已知$\sqrt{x-2}$+y2=y-$\frac{1}{4}$,则xy=1.分析 把$\sqrt{x-2}$+y2=y-$\frac{1}{4}$,化为$\sqrt{x-2}$+(y-$\frac{1}{2}$)2=0,根据非负数的性质求出x与y的值,进而求解即可.
解答 解:∵$\sqrt{x-2}$+y2=y-$\frac{1}{4}$,
∴$\sqrt{x-2}$+y2-y+$\frac{1}{4}$=0,
∴$\sqrt{x-2}$+(y-$\frac{1}{2}$)2=0,
∴x-2=0,y-$\frac{1}{2}$=0,
∴x=2,y=$\frac{1}{2}$,
∴xy=2×$\frac{1}{2}$=1.
故答案为1.
点评 本题考查了配方法的应用及非负数的性质,难度不大,关键是把原式化为$\sqrt{x-2}$+(y-$\frac{1}{2}$)2=0,求出x与y的值.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
14. 如图是从三个方向看到的某个几何体的形状图,则该几何体一定是( )
如图是从三个方向看到的某个几何体的形状图,则该几何体一定是( )
 如图是从三个方向看到的某个几何体的形状图,则该几何体一定是( )
如图是从三个方向看到的某个几何体的形状图,则该几何体一定是( )| A. | 四棱柱 | B. | 三棱柱 | C. | 圆柱 | D. | 圆锥 |

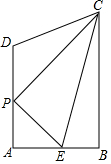 如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,点P在边AD上运动(不与点A,D重合),E是边AB上一点,连结PC,PE,EC.
如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,点P在边AD上运动(不与点A,D重合),E是边AB上一点,连结PC,PE,EC.