题目内容
12. 如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )| A. | 5 | B. | $\sqrt{5}$ | C. | 3 | D. | $\frac{5}{2}$ |
分析 设⊙O的半径为r,在Rt△ACO中,根据勾股定理列式可求出r的值.
解答 解:设⊙O的半径为r,则OA=r,OC=r-1,
∵OD⊥AB,AB=4,
∴AC=$\frac{1}{2}$AB=2,
在Rt△ACO中,OA2=AC2+OC2,
∴r2=22+(r-1)2,
r=$\frac{5}{2}$,
故选D.
点评 本题考查了垂径定理和勾股定理,是常考题型,熟练掌握垂径定理是关键,垂直于弦的直径平分弦;确定一个直角三角形,设未知数,根据勾股定理列方程解决问题.

练习册系列答案
相关题目
3.下列运用等式性质进行的边形,其中不正确的是( )
| A. | 如果a=b,那么a+5=b+5 | B. | 如果a=b,那么a-$\frac{2}{3}$=b-$\frac{2}{3}$ | ||
| C. | 如果ac=bc,那么a=b | D. | 如果$\frac{a}{c}$=$\frac{b}{c}$,那么a=b |
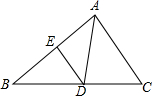 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.