题目内容
2. 己知:如图△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
己知:如图△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.(1)求证:∠DAC=∠DBA;
(2)当AD=3,BD=4时,求⊙O的半径及DE的长.
分析 (1)利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA;
(2)利用勾股定理得出AB的长,再利用三角形面积求出DE即可.
解答 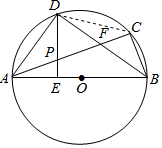 (1)证明:∵BD平分∠CBA,
(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)解:连接CD,
∵∠CBD=∠DBA,
∴CD=AD,
∵CD﹦3,
∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4,即DE的长为2.4.
点评 此题考查的是三角形的外接圆与外心及圆周角定理和勾股定理以及三角形面积等知识,熟练利用圆周角定理得出各等量关系是解题关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
11.下列运算正确的是( )
| A. | 5ab-3ab=2 | B. | x3n÷xn=x3 | C. | (a-b)2=a2-b2 | D. | (-2x2)3=-8x6 |
 如图,D是AB中点,且CB=CD,E为△ABC外一点,满足CE=CA,过点B作BF⊥BC交EA延长线于E.求证:∠FDA=∠BEA.
如图,D是AB中点,且CB=CD,E为△ABC外一点,满足CE=CA,过点B作BF⊥BC交EA延长线于E.求证:∠FDA=∠BEA.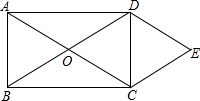 如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证: