题目内容
20.已知二次函数y=a(x-h)2+$\sqrt{3}$的图象经过原点O(0,0),A(2,0),则该函数图象的顶点坐标为(1,$\sqrt{3}$).分析 首先根据二次函数y=a(x-h)2+$\sqrt{3}$的图象经过原点O(0,0),A(2,0)求出对称轴直线x=1,即h=1,进而求出该函数图象的顶点坐标.
解答 解:∵二次函数y=a(x-h)2+$\sqrt{3}$的图象经过原点O(0,0),A(2,0),
∴对称轴直线x=$\frac{0+2}{2}$=1,
∴h=1,
∴该函数图象的顶点坐标为(1,$\sqrt{3}$),
故答案为(1,$\sqrt{3}$).
点评 本题主要考查了二次函数的性质,解答本题的关键是掌握关于对称轴直线对称的两个点的纵坐标相等,此题难度不大.

练习册系列答案
相关题目
11.将抛物线y=2x2+1向左平移1个单位,再向下平移3个单位后所得到的抛物线为( )
| A. | y=2(x+1)2-2 | B. | y=2(x+1)2+4 | C. | y=2(x-1)2-2 | D. | y=2(x-1)2+4 |
15.计算(-3)×2的结果等于( )
| A. | 8 | B. | -6 | C. | 5 | D. | -1 |
5.2cos30°的值等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
9.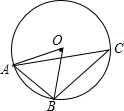 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
 如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )
如图,在⊙O中,∠C=30°,AB=2,则弧AB的长为( )| A. | π | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
10.下列实数中,是无理数的是( )
| A. | -1 | B. | 0 | C. | $\sqrt{2}$ | D. | 3.14 |