题目内容
7.对于a2-2ab+b2-c2的分组中,分组正确的是( )| A. | (a2-c2)+(-2ab+b2) | B. | (a2-2ab+b2)-c2 | C. | a2+(-2ab+b2-c2) | D. | (a2+b2)+(-2ab-c2) |
分析 当被分解的式子是四项时,应考虑运用分组分解法进行分解.本题a2-2ab+b2是完全平方,再可利用平方差公式分解.
解答 解:a2-2ab+b2-c2=(a2-2ab+b2)-c2=(a-b)2-c2=(a-b+c)(a-b-c).
故选B.
点评 本题考查了分组分解法分解因式.注意难点是采用两两分组还是三一分组.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.若a>b,则( )
| A. | a-2<b-2 | B. | 2a<2b | C. | -$\frac{a}{2}$>-$\frac{b}{2}$ | D. | a+5>b+5 |
2.在?ABCD中,∠A:∠B:∠C:∠D的值可以是( )
| A. | 2:3:3:2 | B. | 7:3:7:3 | C. | 7:3:3:2 | D. | 7:3:3:7 |
12. 如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
 如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )
如图,点A,点B,点C在直线l上,则直线,线段,射线的条数分别为( )| A. | 3,3,3 | B. | 1,2,3 | C. | 1,3,6 | D. | 3,2,6 |
19. 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平使A与A′重合,若∠A=35°,则∠1+∠2的度数为( )
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平使A与A′重合,若∠A=35°,则∠1+∠2的度数为( )
 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平使A与A′重合,若∠A=35°,则∠1+∠2的度数为( )
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC上,将△ABC沿着DE折叠压平使A与A′重合,若∠A=35°,则∠1+∠2的度数为( )| A. | 70° | B. | 105° | C. | 140° | D. | 35° |
16.x3n+1可以写成( )
| A. | (x3)n+1 | B. | x3n+x | C. | x•x3n | D. | x6n+1÷x2n |
17. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )| A. | 10° | B. | 15° | C. | 25° | D. | 30° |
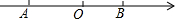 如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0.
如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0.