题目内容
5.已知a,b,c为有理数,且满足a=8-b,c2=ab-16,求a,b,c的值.分析 由a=8-b,c2=ab-16,将其代入ab-c2-16=0得:b2-8b+c2+16=0;此时可发现b2-8b+16正好符合完全平方公式,因此可用非负数的性质求出b、c的值,进而可求得a的值;然后代值运算即可
解答 解:因为a=8-b,c2=ab-16,
所以(8-b)b-c2-16=0.(2分)
即(b-4)2+c2=0.
又(b-4)2≥0,c2≥0,
则b=4,c=0,
所以a=4.
点评 本题既考查了对因式分解方法的掌握,又考查了非负数的性质以及代数式求值的方法.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
15.已知样本数据:1,0,4,1,2;下列说法不正确的是( )
| A. | 众数是1 | B. | 极差是4 | C. | 中位数是4 | D. | 平均数是1.6 |
10.下列命题中,正确的个数是( )
①直径是弦,弦是直径;
②弦是圆上的两点间的部分;
③半圆是弧,但弧不一定是半圆;
④直径相等的两个圆是等圆;
⑤等于半径两倍的线段是直径.
①直径是弦,弦是直径;
②弦是圆上的两点间的部分;
③半圆是弧,但弧不一定是半圆;
④直径相等的两个圆是等圆;
⑤等于半径两倍的线段是直径.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.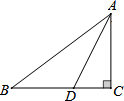 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )| A. | ($\sqrt{2}$-1):1 | B. | ($\sqrt{2}$+1):1 | C. | $\sqrt{2}$:1 | D. | 2:1 |