题目内容
8.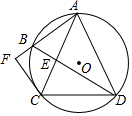 如图,四边形ABCD是⊙O的内接四边形,∠ABD=∠CBD=60°,AC与BD相交于点E,过点C作⊙O的切线,与AB的延长线相交于点F.
如图,四边形ABCD是⊙O的内接四边形,∠ABD=∠CBD=60°,AC与BD相交于点E,过点C作⊙O的切线,与AB的延长线相交于点F.(1)判断△ACD的形状,并加以证明
(2)若CF=2,DE=4,求弦CD的长.
分析 (1)根据圆周角定理即可得到结论;
(2)根据全等三角形的性质得到AF=DE=4,CE=CF=2,根据切线的性质得到FC2=FB•AF,求得FB=1根据相似三角形的性质即可得到结论;
解答 解:(1)∵∠ABD=∠CBD=60°,
∴∠CAD=∠CBD=60°,∠ACD=∠ABD=60°,
∴△ACD是等边三角形;
(2)在△ACF与△DCE中,$\left\{\begin{array}{l}{∠CDE=∠FAC}\\{∠ACF=∠ACD}\\{AC=CD}\end{array}\right.$
∴△ACF≌△DCE,
∴AF=DE=4,CE=CF=2,
∵CF是⊙O的切线,
∴FC2=FB•AF,
∴22=FB•4,
∴FB=1
∴AB=AF-BF=4-1=3,
∵∠ABE=∠DCE,∠BAE=∠CDE,
∴△∠ABE∽∠DCE,
∴$\frac{AB}{CD}$=$\frac{BE}{DE}$=$\frac{AE}{CE}$=$\frac{CD-CE}{CE}$,
∴$\frac{3}{CD}$=$\frac{CD-2}{2}$,
解得:CD=3.
点评 本题考查了切线的性质,全等三角形的判定和性质,相似三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
19.设m,n分别为一元二次方程x2+2x-2018=0的两个实数根,则m2+3m+n=( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
16.如果n与-3互为相反数,则n的值为( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
3.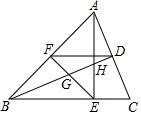 如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )
如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )
 如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )
如图,在△ABC中,AE和BD是高,∠ABE=45°,点F是AB的中点,BD与FE,AE分别交于点G、H,∠CAE=∠ABD.有下列结论:①FD=FE;②BH=2CD;③BD•BH=2BE2;④S△ABC=$\frac{4}{3}$S四边形BCDF.其中正确的有( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②④ |
20.在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.下列图形中主视图,左视图不相同的是( )
| A. |  | B. |  | C. |  | D. |  |
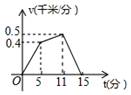
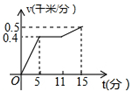

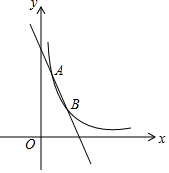 如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.