题目内容
17.用棋子按下列方式摆图形,第一个图形有1个棋子,第二个图形有5个棋子,第三个图形有12个棋子,依次规律,第六个有( )枚棋子.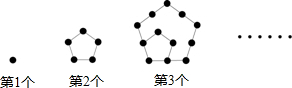
| A. | 49 | B. | 50 | C. | 51 | D. | 52 |
分析 由图形可知:第一个图形有1个棋子,第二个图形有1+4=5个棋子,第三个图形有1+4+7=12个棋子,…由此得出第n个图形有1+4+7+…+(3n-2)=$\frac{1}{2}$n(3n-1)个棋子,进一步代入求得答案即可.
解答 解:∵第一个图形有1个棋子,
第二个图形有1+4=5个棋子,
第三个图形有1+4+7=12个棋子,
…
∴第n个图形有1+4+7+…+(3n-2)=$\frac{1}{2}$n(3n-1)个棋子,
∴第六个有$\frac{1}{2}$×6×(3×6-1)=51枚棋子.
故选:C.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字的运算规律解决问题.

练习册系列答案
相关题目
5.点P关于x轴对称的点是(3,-4),则点P关于y轴对称的点的坐标在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
12.实数-8的相反数是( )
| A. | 4 | B. | 8 | C. | -8 | D. | 0 |
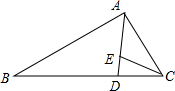 如图,在△ABC中,若∠DAC=∠B.
如图,在△ABC中,若∠DAC=∠B.