题目内容
2．将一个半径为3cm的圆分成四个扇形，它们的圆心角的度数之比为2：3：3：4，则最大扇形的面积为$\frac{4π}{3}$cm2．分析 分别求出四个扇形圆心角，圆心角最大的扇形的面积最大，进而利用扇形面积求法得出即可．
解答 解：∵一个圆分割成四个扇形，它们的圆心角的度数比为2：3：4：3，
∴它们的圆心角的度数分别为：60°，90°，120°，90°，
圆心角位120°的扇形的面积最大，其面积为：$\frac{120π×{2}^{2}}{360}$=$\frac{4π}{3}$（cm2）．
故答案是：$\frac{4π}{3}$cm2．
点评 此题主要考查了认识平面图形、扇形面积求法，正确记忆扇形面积公式是解题关键．
练习册系列答案
快捷英语周周练系列答案
相关题目
如图，点A（t，4）在第一象限，OA与x轴所夹的锐角为α，tanα=$\frac{4}{3}$，则t的值为3．
7．
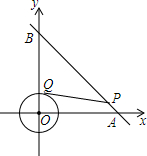如图，⊙O是以原点为圆心，2为半径的圆，点P是直线y=-x+4上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）
如图，⊙O是以原点为圆心，2为半径的圆，点P是直线y=-x+4上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）| A． | 3 | B． | 2 | C． | 3-$\sqrt{2}$ | D． | 2 $\sqrt{2}$ |
14．下列四个图形中，是中心对称图形的为（ ）
| A． |  | B． |  | C． |  | D． |  |
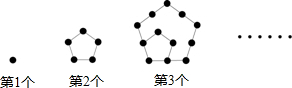
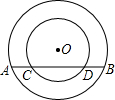如图，在以O为圆心的同心圆中，大圆的弦AB交小圆于C、D，AB=2CD，弦AB的弦心距OP=$\frac{1}{2}$CD，小圆和大圆半径分别为r、R，则$\frac{r}{R}$=$\frac{\sqrt{10}}{5}$．