��Ŀ����
�Ķ�����
������y=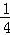 x2������һ�㵽�㣨0��1���ľ����뵽ֱ��y=﹣1�ľ�����ȣ������������һ���ʽ�����⣮
x2������һ�㵽�㣨0��1���ľ����뵽ֱ��y=﹣1�ľ�����ȣ������������һ���ʽ�����⣮
������
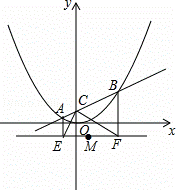
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+1��y�ύ��C�㣬�뺯��y=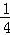 x2��ͼ����A��B���㣬�ֱ��A��B������ֱ��y=﹣1�Ĵ��ߣ�����E��F���㣮
x2��ͼ����A��B���㣬�ֱ��A��B������ֱ��y=﹣1�Ĵ��ߣ�����E��F���㣮
��1��д����C�����꣬��˵����ECF=90�㣻
��2���ڡ�PEF�У�MΪEF�е㣬PΪ���㣮
����֤��PE2+PF2=2��PM2+EM2����
����֪PE=PF=3����EFΪһ���Խ�����ƽ���ı���CEDF����1��PD��2������CP��ȡֵ��Χ��
�⣺��1����x=0ʱ��y=k•0+1=1��
���C��������0��1����
��������ɵã�AC=AE��
���AEC=��ACE��
��AE��EF��CO��EF��
��AE��CO��
���AEC=��OCE��
���ACE=��OCE��
ͬ���ɵã���OCF=��BCF��
�ߡ�ACE+��OCE+��OCF+��BCF=180�㣬
��2��OCE+2��OCF=180�㣬
���OCE+��OCF=90�㣬����ECF=90�㣻
��2���ٹ���P��PH��EF��H��
������H���߶�EF�ϣ���ͼ2�٣�
��MΪEF�е㣬
��EM=FM= EF��
EF��
���ݹ��ɶ����ɵã�
PE2+PF2﹣2PM2=PH2+EH2+PH2+HF2﹣2PM2
=2PH2+EH2+HF2﹣2��PH2+MH2��
=EH2﹣MH2+HF2﹣MH2
=��EH+MH����EH﹣MH��+��HF+MH����HF﹣MH��
=EM��EH+MH��+MF��HF﹣MH��
=EM��EH+MH��+EM��HF﹣MH��
=EM��EH+MH+HF﹣MH��
=EM•EF=2EM2��
��PE2+PF2=2��PM2+EM2����
������H���߶�EF���ӳ��ߣ������ӳ��ߣ��ϣ���ͼ2�ڣ�
ͬ���ɵã�PE2+PF2=2��PM2+EM2����
��������������H��ֱ��EF��ʱ������PE2+PF2=2��PM2+EM2����
������CD��PM����ͼ3��
�ߡ�ECF=90�㣬
��▱CEDF�Ǿ��Σ�
��M��EF���е㣬
��M��CD���е㣬��MC=EM��
�ɢ��еĽ��ۿɵã�
�ڡ�PEF�У���PE2+PF2=2��PM2+EM2����
�ڡ�PCD�У���PC2+PD2=2��PM2+CM2����
��MC=EM��
��PC2+PD2=PE2+PF2��
��PE=PF=3��
��PC2+PD2=18��
��1��PD��2��
��1��PD2��4��
��1��18﹣PC2��4��
��14��PC2��17��
��PC��0��
�� ��PC��
��PC�� ��
��





 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д� ��
�� ���������
Ϊ������λ���� Ϊ
Ϊ �Ĺ�����������н�����ȷ����
�Ĺ�����������н�����ȷ���� B.
B.  C.
C. D.
D.





 �Ľ�����
�Ľ����� �Ľ⼯Ϊ
�Ľ⼯Ϊ ����
���� ��ֵΪ�� ��
��ֵΪ�� �� D��
D��