题目内容
4. 如图,在Rt△ABC中∠A=90°,甲、乙二人从点D同时出发,甲沿DA,AB过桥到达点B处,乙沿DC过桥由点C直达B处.已知DA=6千米,AB=6千米,DC=2千米,假设甲、乙两人的速度相同,问:甲、乙二人谁先到达B处?说明理由.
如图,在Rt△ABC中∠A=90°,甲、乙二人从点D同时出发,甲沿DA,AB过桥到达点B处,乙沿DC过桥由点C直达B处.已知DA=6千米,AB=6千米,DC=2千米,假设甲、乙两人的速度相同,问:甲、乙二人谁先到达B处?说明理由.
分析 先根据勾股定理求出BC的长,再比较CD+BC与AD+AB的大小即可.
解答 解:∵DA=6千米,AB=6千米,DC=2千米,
∴BC=$\sqrt{A{C}^{2}+A{B}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10(千米),
∴DC+BC=2+10=12(千米),AD+AB=6+6=12(千米),
∴DC+BC=AD+AB,
∴甲、乙二人同时到达B处.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
16.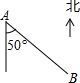 如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
 如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )| A. | 南偏东50° | B. | 南偏东50°且距货轮40 nmile处 | ||
| C. | 距灯塔40 nmile处 | D. | 北偏西50°且距货轮40 nmile处 |

 如图,AC=AE,∠1=∠2,AB=AD,求证:∠B=∠D.
如图,AC=AE,∠1=∠2,AB=AD,求证:∠B=∠D.