题目内容
9.对x,y定义一种新运算T,规定:T(x,y)=$\frac{ax+by}{x+y}$(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=$\frac{a×0+b×1}{0+1}$=b,已知T(1,1)=2.5,T(4,-2)=4.(1)求a,b的值;
(2)若关于m的不等式组$\left\{\begin{array}{l}{T(4m,5-4m)≤3}\\{T(2m,3-2m)>P}\end{array}\right.$恰好有2个整数解,求实数P的取值范围.
分析 (1)根据题中的新定义列出关于a与b的方程组,求出方程组的解即可得到a与b的值;
(2)利用题中的新定义化简已知不等式组,求出解集,根据关于m的不等式组恰好有2个整数解,确定p的范围即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a+b=5①}\\{2a-b=4②}\end{array}\right.$,
①+②得:3a=9,即a=3,
把a=3代入①得:b=2,
故a,b的值分别为3和2;
(2)根据题意得:$\left\{\begin{array}{l}{\frac{12m+10-8m}{5}≤3①}\\{\frac{6m+6-4m}{3}>p②}\end{array}\right.$,
由①得:m≤$\frac{5}{4}$,
由②得:m>$\frac{3}{2}$p-3,
∴不等式组的解集为$\frac{3}{2}$p-3<m≤$\frac{5}{4}$,
∵不等式组恰好有2个整数解,即m=0,1,
∴-1≤$\frac{3}{2}$p-3<0,
解得$\frac{4}{3}$≤p<2,
即实数P的取值范围是$\frac{4}{3}$≤p<2.
点评 本题主要考查了解二元一次方程组以及解一元一次不等式组,理解题中的新定义,并熟练掌握一元一次不等式组的解法是解本题的关键.

练习册系列答案
相关题目
17.超市为减小A商品的积压,决定采取降价销售的策略,若某商品的原价为52元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
(1)这个表反映了降价和日销量两个变量之间的关系;
(2)从表中可以看出每降价1元,日销量增加5件;
(3)可以估计降价之前的日销量为150件;
(4)设日销量为y件,降价为x元,则y与x的函数关系式为y=5x+150;
(5)当售价为44元时,日销量为190件.
| 降价(元) | 1 | 2 | 3 | 4 | 5 | 6 |
| 日销量(件) | 155 | 160 | 165 | 170 | 175 | 180 |
(2)从表中可以看出每降价1元,日销量增加5件;
(3)可以估计降价之前的日销量为150件;
(4)设日销量为y件,降价为x元,则y与x的函数关系式为y=5x+150;
(5)当售价为44元时,日销量为190件.
19.下列关于无理数的说法,错误的是( )
| A. | 无理数是实数 | B. | 无理数是无限不循环小数 | ||
| C. | 无理数是无限小数 | D. | 无理数是带根号的数 |
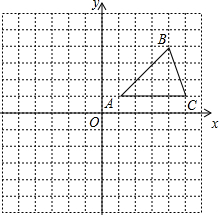 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).