Question

2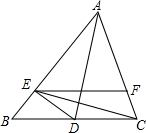．如图，AD是△ABC的角平分线，且AE=AC，EF∥BC交AC于点F，∠DEC=∠DCE=∠FEC．

Answer 1

分析 根据等腰三角形的性质得到AD是EC的垂直平分线，得到DE=DC，根据等腰三角形的性质得到∠DEC=∠DCE，根据平行线的性质得到∠DCE=∠FEC即可证明结论．

解答 解：∵AD是△ABC的角平分线，且AE=AC，
∴AD是EC的垂直平分线，
∴DE=DC，
∴∠DEC=∠DCE，
∵EF∥BC，
∴∠DCE=∠FEC，
∴∠DEC=∠DCE=∠FEC，
故答案为：DCE；FEC．

点评 本题考查的是等腰三角形的性质和平行线的性质，掌握等腰三角形的三线合一是解题的关键．