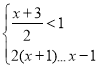Question

【题目】在四边形 ABCD 中，BD 平分∠ABC．

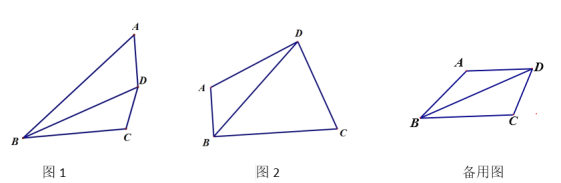
（1）如图 1，若∠BAD=∠BDC，求证：BD2=ABBC；

（2）如图 2，∠A>90°，∠BAD+∠BDC=180°，

①若∠ABC=90°，AB=，BC=8，求BD的长；

②若 BC=3CD=3a，BD=9， 则 AB 的长为 ． (用含 a 的代数式表示)．

Answer 1

【答案】（1）详见解析；（2）①；②

【解析】

（1）先利用角平分线得出，进而得出，即可得出结论；

（2）①先做辅助线，延长BA到点M，使BM=BC，先证明，之后再证明来求到DM，最后连接CM构造等腰直角三角形求出BO和OD，即可得出结论；②同（2）的方法做辅助线，延长BA到点M，使BM=BC，再利用和即可得出结论．

解：（1）是∠ABC的平分线，

，

，

，

，

；

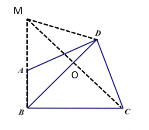
（2）①如图，延长BA到点M，使BM=BC，

是∠ABC的平分线，

,

，

(SAS)，

则,BM=BC=8，DM=DC，

,

，

,

即,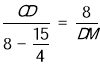

解得：DM=DC=，

连接MC与BD交于点O，

∵∠MBC=90°，BC=BM=8，

∴为等腰直角三角形，

∵BO平分∠MBC，

∴BD⊥MC，BO=CO=MO=，

在直角中，

,

；

故答案为：；

②如图，延长BA到点M，使BM=BC，

连接DM，

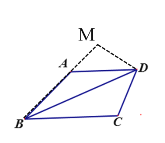
∵BC=3CD=3a，

，

同（2）①可证，，

，

,

即，

，

，

故答案为：．