题目内容
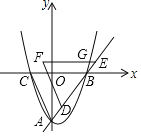
【题目】如图，平面直角坐标系中，直线
与
轴、
轴分别交于点
、
，直线
与轴、轴分别交于点
、
，与相交于点
，线段
、
的长是一元二次方程
的两根
，
，点的横坐标为3，反比例函数
的图象经过点．
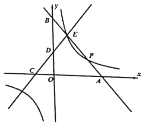
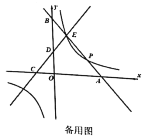
（1）若直线与反比例函数图象上除点外的另一交点为
，求
的面积；若点
在轴上，若点
在轴上，求
的最小值．．
（2）若点
在坐标轴上，在平面内是否存在一点
，使以点、、、为顶点的四边形是矩形且线段
为矩形的一条边？若存在，直接写出符合条件的点坐标；若不存在，请说明理由．
【答案】（1）72；20
（2）答案见解析
【解析】
（1）先解一元二次方程，得出OA，OC，即可得出点A和点C坐标，进而求出OB得出B点坐标，求出直线AB解析式，即可求出点E坐标，再求出点P坐标，再用面积差求出
的面积.
作点P关于x轴的对称点
，点E关于y轴的对称点
，
就是
的最小值，求出即可.
（2）先确定直线CE解析式，
、
、
、
为顶点的四边形是矩形作为已知条件，作满足条件的辅助线，根据两条直线垂直，它们的k值相乘等于-1，两条直线平行k值相等且经过已知点，可求出直线解析式，再利用两条直线相交，y值相等，列出关于x的等式，求出交点坐标，即为所求.
（1）∵线段
、
的长是一元二次方程
的两根
∴OC=6，OA=12，
∴
=16
∴B(0，16)
设直线AB的解析式为
∴
∴直线AB的解析式为
∵点的横坐标为3，且在直线AB上
得E(3，12)
又∵点E在反比例函数
∴k=36
设点P横坐标为m纵坐标就为
∵点P在反比例函数上
∴
∴
（舍）或
∴P(9，4)
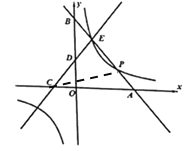
如图作点P关于x轴的对称点，点E关于y轴的对称点
∵P(9，4)，E(3，12)
∴ (9，-4)，（-3，12）
连接交x轴于R，交y轴于S，此时最小
最小值=
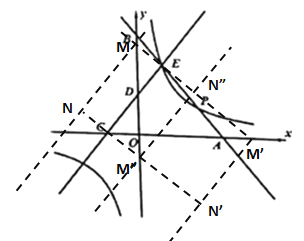
(2)由（1）知
∴直线CE的解析式为
∵、、、为顶点的四边形是矩形且线段
为矩形的一条边
过点E作
垂直于CE交x轴于
交y轴于M
已知（-3，12）
∴直线的解析式为
过点M作
∥CE，过点C作
∴直线MN的解析式为
∵C(-6，0)
∴直线CN的解析式为
N点是直线MN和CN的交点设N（m，n）
m=-9，n=
N(-9， )
过点作
交直线CN于
∴直线
的解析式为
联合直线CN的解析式为
得
过
作
交于
∵直线CN的解析式为，
∴直线
的解析式为
联合直线的解析式为
∴
∴所以满足条件的N点的坐标为(-9， )，
或
【题目】今年是五四运动100周年，也是中华人民共和国成立70周年，为缅怀五四先驱崇高的爱国情怀和革命精神，巴蜀中学开展了“青春心向党，建功新时代”为主题的系列纪念活动．历史教研组也组织了近代史知识竞赛，七、八年级各有300名学生参加竞赛．为了解这两个年级参加竞赛学生的成绩情况，从中各随机抽取20名学生的成绩，并对数据进行了整理和分析（成绩得分用
表示，数据分为6组
；
；
；
；
；
）
绘制了如下统计图表：
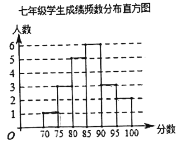
年级 | 平均数 | 中位数 | 众数 | 极差 |
七年级 | 85.8 |
|
| 26 |
八年级 | 86.2 | 86.5 | 87 | 18 |
七年级测试成绩在
、
两组的是：81 83 83 83 83 86 87 88 88 89 89
根据以上信息，解答下列问题
（1）上表中
_______，
_______．
（2）记成绩90分及90分以上为优秀，则估计七年级参加此次知识竞赛成绩为优秀的学生有多少名？
（3）此次竞赛中，七、八两个年级学生近代史知识掌握更好的是________（填“七”或“八“）年级，并说明理由？
