题目内容
20. 如图,C,D是半圆O上的点,弦AC,BD相交于点E,连接CD,若直径AB=2,CE=$\sqrt{3}$BC,则阴影部分面积为$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$.
如图,C,D是半圆O上的点,弦AC,BD相交于点E,连接CD,若直径AB=2,CE=$\sqrt{3}$BC,则阴影部分面积为$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$.
分析 连接OC,OD,过点O作OF⊥CD于点F,根据圆周角定理得出∠ACB=90°,再由CE=$\sqrt{3}$BC可知∠CBE=60°,故可得出∠COD的度数,根据等腰三角形的性质得出∠OCD的度数,由锐角三角函数的定义求出CF及OF的长,利用S阴影=S扇形DOC-S△DOC即可得出结论.
解答 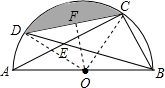 解:连接OC,OD,过点O作OF⊥CD于点F,
解:连接OC,OD,过点O作OF⊥CD于点F,
∵AB是直径,
∴∠ACB=90°.、
∵CE=$\sqrt{3}$BC,
∴∠CBE=60°,
∴∠COD=120°.
∵OD=OC,
∴∠ODC=∠OCD=30°,
∴CF=$\frac{\sqrt{3}}{2}$,OF=$\frac{1}{2}$,
∴CD=2CF=$\sqrt{3}$
∴S阴影=S扇形DOC-S△DOC=$\frac{120π×{1}^{2}}{360}$-$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15. 如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
 如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}π}{3}$ | D. | $\sqrt{3}$π |
12.已知x=3时,分式$\frac{3x+k}{x-1}$的值等于0,则k的值为( )
| A. | 9 | B. | -9 | C. | -3 | D. | 3 |
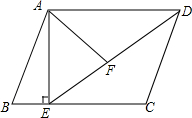 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.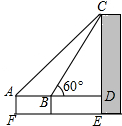 如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m).
如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m).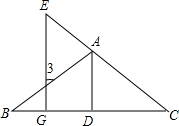 如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.
如图,已知AD⊥BC,EG⊥BC,D、G分别是垂足,如果∠GEC=∠3,那么AD平分∠BAC吗?试写出推理全过程.