题目内容
6.将下列数轴上的x的范围用不等式表示出来
(1)$\left\{\begin{array}{l}x≤-2\\ x≤1\end{array}\right.$
(2)$\left\{\begin{array}{l}x<-2\\ x>1\end{array}\right.$.
分析 (1)根据1、-2两点处是实心圆点且折线向左可得出不等式组;
(2)根据1处是实心圆点且折线,-2处是实心圆点且折线向左可得出不等式组.
解答 解:(1)∵1、-2两点处是实心圆点且折线向左,
∴不等式为$\left\{\begin{array}{l}x≤-2\\ x≤1\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}x≤-2\\ x≤1\end{array}\right.$;
(2)∵1处是实心圆点且折线,-2处是实心圆点且折线向左,
∴不等式为$\left\{\begin{array}{l}x<-2\\ x>1\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}x<-2\\ x>1\end{array}\right.$.
点评 本题考查的是在数轴上表示不等式的解集,熟知实心圆点与空心圆点的区别是解答此题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14.下列说法错误的是( )
| A. | 0是最小的整数 | B. | 1是最小的正整数 | C. | 0是最小的自然数 | D. | 自然数是非负数 |
18.若(a+1)xa2+1+3ax-2=0是关于x的一元二次方程,则a值为( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
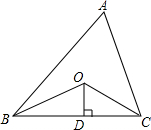 如图所示,已知△ABC的面积是26,AB+AC=20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则BC的长是6.
如图所示,已知△ABC的面积是26,AB+AC=20,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=2,则BC的长是6.
 如图,在梯形ABCD中,AD∥BC,AC、BD相交于点E,S△ADE:S△ADC=1:3,那么S△ADE:S△CBE=1:4.
如图,在梯形ABCD中,AD∥BC,AC、BD相交于点E,S△ADE:S△ADC=1:3,那么S△ADE:S△CBE=1:4.