题目内容
12.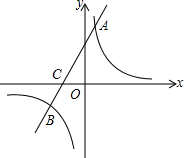 如图,在平面直角坐标系中,一次函数y=2x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).
如图,在平面直角坐标系中,一次函数y=2x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,与x轴交于点C(-2,0),点A的坐标为(n,6).(1)求该反比例函数的解析式;
(2)求点B的坐标,写出一次函数值大于反比例函数值时自变量x的取值范围;
(3)若点E为x轴上使△ACE为直角三角形的一点,求点E的坐标.
分析 (1)利用待定系数法求得一次函数表达式,进而求得A( 1,6),代入y=$\frac{k}{x}$(k≠0)利用待定系数法即可求得.
(2)联立方程,解方程组即可求得B的坐标,根据交点坐标即可求得一次函数值大于反比例函数值时自变量x的取值范围;
(3)分两种情况分别讨论即可求得.
解答 解:(1)∵C(-2,0)在直线 y=2x+b 上,解得b=4,
∴一次函数表达式为 y=2x+4,
∵A( n,6)在直线 y=2x+4 上,解得n=1
∴A( 1,6)
又∵点A( 1,6)在反比例函数图象上,解得k=6
∴反比例函数表达式为 y=$\frac{6}{x}$;
( 2)由$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=2x+4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{2}=6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-2}\end{array}\right.$
∴A( 1,6)B(-3,-2).
由图象知,一次函数值大于反比例函数值时自变量x的取值范围为-3<x<0或x>1;
( 3)∵∠ACE为锐角,
∴分两种情况讨论:
①∠AEC=90°时,E1 ( 1,0)
②∠EAC=90°时,△ACE1∽△AE1E2
∴AE12=CE1•E1E2
∴62=3E1E2
∴E1E2=12
∴E2 ( 13,0)
综上所述E1 ( 1,0)E2 ( 13,0).
点评 此题考查了反比例函数与一次函数的交点问题.其知识点有待定系数法求解析式,三角形相似的判定和性质,解方程组等,此题难度适中,注意掌握数形结合思想与方程思想的应用.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+6+6+8+10=30=5×6 |
| … | … |
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+6…+2n=n(n+1);
(3)根据(2)题的公式,计算:102+104+106+…+2012+2014.
| A. | 日光灯管厂要检测一批灯管的使用寿命 | |
| B. | 了解嘉兴市每天的流动人口数 | |
| C. | 了解浙江省城市居民日平均用水量 | |
| D. | 旅客上飞机前的安全检查 |
 如图,直线AB,CD相交于O,OE平分∠AOC,∠EOC=40°,则∠BOD=( )
如图,直线AB,CD相交于O,OE平分∠AOC,∠EOC=40°,则∠BOD=( )| A. | 40° | B. | 80° | C. | 50° | D. | 100° |
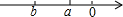 如图,a,b所在数轴的位置,化简下列各式:
如图,a,b所在数轴的位置,化简下列各式:
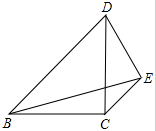 如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.
如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$. 图中有多少个三角形?
图中有多少个三角形?