题目内容
4.计算.①(-2)3+$\sqrt{{{({-4})}^2}}+\root{3}{{{{(-4)}^3}}}×{({-\frac{1}{2}})^2}-\root{3}{27}$.
②(x-1)2=9
③(x+1)3=-125
④$\left\{\begin{array}{l}5m+n=7\\ 4m-2n=4\end{array}$
⑤$\left\{\begin{array}{l}\frac{x}{3}-\frac{y+1}{6}=1\\ 3x+2y=0\end{array}$.
分析 ①分别根据数的乘方及开方法则计算出各数,再根据实数混合运算的法则进行计算即可;
②、③利用直接开方法求出x的值即可;
④先用加减消元法求出m的值,再用代入消元法求出n的值即可;
⑤先把方程组中的方程化为不含分母及括号的方程,再用加减消元法或代入消元法求解即可.
解答 解:①原式=-8+4-4×$\frac{1}{4}$-3;
=-4-1-3
=-8;
②方程两边直接开方得,x-1=±3,解得x1=4,x2=-2;
③方程两边直接开方得,x+1=-5,解得x=-6;
④$\left\{\begin{array}{l}5m+n=7①\\ 4m-2n=4②\end{array}\right.$,①×2+②得,14m=18,解得m=$\frac{9}{7}$,把m=$\frac{9}{7}$代入①得,n=$\frac{4}{7}$,
故方程组的解为$\left\{\begin{array}{l}m=\frac{9}{7}\\ n=\frac{4}{7}\end{array}\right.$;
⑤原方程组可化为$\left\{\begin{array}{l}2x-y=7①\\ 3x+2y=0②\end{array}\right.$,①×2+②得,7x=14,解得x=2.把x=2代入①得,4-y=7,解得y=-3,
故方程组的解为$\left\{\begin{array}{l}x=2\\ y=-3\end{array}\right.$.
点评 本题考查的是实数的运算,熟知数的开方法则及绝对值的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.据北京市气象局统计,今年的雾霾天气比常年同期多一倍以上,为1954年以来同期最多,表一是国家环保总局所公布的空气质量级别表.现从市环保监测站提供的资料中,随机抽取了今年1至3月份中30天空气综合的污染指数如下:
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167,
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243.
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)先填写频率分布表二中未完成的空格,并求出统计数据中的中位数和众数;
(2)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良的天数.
空气质量级别表一
频率分布表二
30,32,40,42,45,45,77,83,85,87,90,113,127,153,167,
38,45,48,53,57,64,66,77,92,98,130,184,201,235,243.
请根据空气质量级别表和抽查的空气综合污染指数,解答以下问题:
(1)先填写频率分布表二中未完成的空格,并求出统计数据中的中位数和众数;
(2)请根据抽样数据,估计该市今年(按360天计算)空气质量是优良的天数.
空气质量级别表一
| 空气污染指数 | 空气质量 | 级别 |
| 0-50 | 一级 | 优 |
| 51-100 | 二级 | 良 |
| 101-150 | 三级 | 轻度污染 |
| 151-200 | 四级 | 中度污染 |
| 201-300 | 五级 | 重度污染 |
| >300 | 六级 | 严重污染 |
| 分组 | 频数 | 频率 |
| 0-50 | 0.30 | |
| 51-100 | 12 | 0.40 |
| 101-150 | ||
| 151-200 | 3 | 0.10 |
| 201-300 | 3 | 0.10 |
| 300 | 0 | 0.00 |
| 合计 | 30 | 1.00 |
9.已知xy≠1,且有3x2+2014x+7=0,7y2+2014y+3=0,则$\frac{x}{y}$的值等于( )
| A. | $\frac{3}{7}$ | B. | $\frac{7}{3}$ | C. | -$\frac{2014}{7}$ | D. | -$\frac{2014}{3}$ |
 如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为120°.
如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为120°. 如图所示,线段AP上有两点M、N,AM:MP=5:11,AN:NP=5:7,MN=2.5,则AP长度是24.
如图所示,线段AP上有两点M、N,AM:MP=5:11,AN:NP=5:7,MN=2.5,则AP长度是24.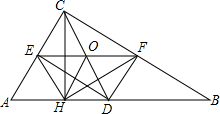 已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.
已知:如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别是AB,AC,BC的中点,点H在AB上,且∠EHF=90°,求证:CH⊥AB.