题目内容
11．
如图，已知扇形AOB的半径为6，圆心角为90°，连接AB，则图中阴影部分的面积是π-2．
分析 由∠AOB为90°，得到△OAB为等腰直角三角形，于是OA=OB，而S阴影部分=S扇形OAB-S△OAB．然后根据扇形和直角三角形的面积公式计算即可．
解答 解：S阴影部分=S扇形OAB-S△OAB
=$\frac{90π×{2}^{2}}{360}$-$\frac{1}{2}$×2×2
=π-2
故答案是：π-2．
点评 本题考查了扇形面积的计算，是属于基础性的题目的一个组合，只要记住公式即可正确解出．关键是从图中可以看出阴影部分的面积是扇形的面积减去直角三角形的面积．
练习册系列答案
相关题目
2．若2b2nam与-5ab6的和仍是一个单项式，则m、n值分别为（ ）
| A． | 6，$\frac{1}{2}$ | B． | 1，2 | C． | 1，3 | D． | 2，3 |
16．
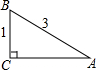坡比常用来反映斜坡的倾斜程度，如图所示，斜坡AB的坡比为（ ）
坡比常用来反映斜坡的倾斜程度，如图所示，斜坡AB的坡比为（ ）| A． | 1：2$\sqrt{2}$ | B． | 2$\sqrt{2}$：1 | C． | 1：3 | D． | 3：1 |
20．4的平方根是（ ）
| A． | 2 | B． | 4 | C． | ±2 | D． | ±$\sqrt{2}$ |
1．
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．AC=3，AB=6，则AD=（ ）
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D．AC=3，AB=6，则AD=（ ）| A． | $\frac{3}{2}$ | B． | 3 | C． | $\frac{9}{2}$ | D． | 3$\sqrt{3}$ |