题目内容
1.设n=$\frac{2}{x+3}$+$\frac{2}{3-x}$$+\frac{2x+18}{{x}^{2}-9}$,若n的值为整数,则x可以取的值的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 先通分,再加减,最后化简.根据化简结果为整数,确定x的取值个数.
解答 解:n=$\frac{2}{x+3}$+$\frac{2}{3-x}$$+\frac{2x+18}{{x}^{2}-9}$
=$\frac{2(x-3)}{(x+3)(x-3)}$-$\frac{2(x+3)}{(x+3)(x-3)}$+$\frac{2x+18}{(x+3)(x-3)}$
=$\frac{2x-6-2x-6+2x+18}{(x+3)(x-3)}$
=$\frac{2(x+3)}{(x+3)(x-3)}$
=$\frac{2}{x-3}$
当x-3=±1、±2,即x=4、2、1、5时
分式$\frac{2}{x+3}$的值为整数.
故选B.
点评 本题考查了异分母分式的加减法及分式为整数的相关知识.解决本题的关键是根据化简结果得到分式值为整数的x的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( )


| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
 如图,在梯形ABCD中,AB∥DC,AC、BD相交于点O,如果S三角形AOB=16cm2,S三角形COD=9cm2,则S三角形DOC:S三角形COB=3:4.
如图,在梯形ABCD中,AB∥DC,AC、BD相交于点O,如果S三角形AOB=16cm2,S三角形COD=9cm2,则S三角形DOC:S三角形COB=3:4.




 如图,点A是双曲线y=$\frac{6}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为底作等腰△ABC,使∠C=120°,且点C在第四象限内,且随着点A的运动,点C的位置也不断变化.但点C始终也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是( )
如图,点A是双曲线y=$\frac{6}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为底作等腰△ABC,使∠C=120°,且点C在第四象限内,且随着点A的运动,点C的位置也不断变化.但点C始终也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是( )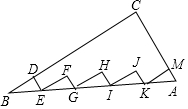 如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24.
如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为24. 如图,已知扇形AOB的半径为6,圆心角为90°,连接AB,则图中阴影部分的面积是π-2.
如图,已知扇形AOB的半径为6,圆心角为90°,连接AB,则图中阴影部分的面积是π-2.