Question

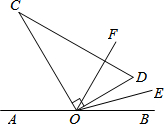如图，点O为直线AB上一点，将直角三角板OCD的直角顶点放在点O处．已知∠AOC的度数比∠BOD的度数的3倍多10度．
（1）求∠BOD的度数．
（2）若OE、OF分别平分∠BOD、∠BOC，求∠EOF的度数．（写出必要的推理过程）

Answer 1

解：（1）设∠BOD=x°，
∵∠AOC的度数比∠BOD的度数的3倍多10度，且∠COD=90°，
∴x+（3x+10）+90=180，
解得：x=20，
∴∠BOD=20°；

（2）∵OE、OF分别平分∠BOD、∠BOC，
∴∠BOE=∠BOD，∠BOF=∠BOC=（∠BOD+∠COD），
∴∠EOF=∠BOF-∠BOE=∠COD=45°．
分析：（1）首先设∠BOD=x°，由∠AOC的度数比∠BOD的度数的3倍多10度，且∠COD=90°，可得方程：x+（3x+10）+90=180，解此方程即可求得答案；
（2）由OE、OF分别平分∠BOD、∠BOC，可得∠BOE=∠BOD，∠BOF=∠BOC=（∠BOD+∠COD），又由∠EOF=∠BOF-∠BOE=∠COD，即可求得答案．
点评：此题考查了角的计算与角平分线的定义．此题难度适中，注意掌握数形结合思想与方程思想的应用．