题目内容
16.已知二元一次方程组$\left\{\begin{array}{l}{ax+by=7}\\{bx-ay=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,求4a-3b的值.分析 首先把$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$代入$\left\{\begin{array}{l}{ax+by=7}\\{bx-ay=5}\end{array}\right.$得关于a、b的方程组,解方程组可得a、b的值,进而可得4a-3b的值.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$代入$\left\{\begin{array}{l}{ax+by=7}\\{bx-ay=5}\end{array}\right.$得:$\left\{\begin{array}{l}{a-2b=7}\\{b+2a=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{17}{5}}\\{b=-\frac{9}{5}}\end{array}\right.$,
4a-3b=4×$\frac{17}{5}$+3×$\frac{9}{5}$=19.
点评 此题主要考查了二元一次方程组的解,关键是掌握二元一次方程组的解能同时是两个方程成立.

练习册系列答案
相关题目
6.不等式4(x-1)<3x-2的正整数解的个数为( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
7.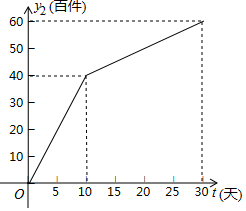 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
4.下列各组数中互为相反数的是( )
| A. | -2与-$\frac{1}{2}$ | B. | 2与|-2| | C. | -2与$\root{3}{-8}$ | D. | -2与$\sqrt{(-2)^{2}}$ |
1. 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表
根据以上信息,解决下列问题:
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
 某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某初中校对学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:各年级学生成绩统计表
| 各年级学生成绩统计表 | ||||
| 优秀 | 良好 | 合格 | 不合格 | |
| 七年级 | 28 | 20 | a | 8 |
| 八年级 | 29 | 13 | 13 | 5 |
| 九年级 | 24 | 15 | 14 | b |
(1)在统计表中,a的值为24,b的值为7;
(2)在扇形统计图中,八年级所对应的扇形圆心角为108°;
(3)若该校三个年级共2000名学生参加考试,试估计其中体育成绩不合格的人数.
11.将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
12.在同一坐标系中,抛物线y=x2,y=-x2,y=$\frac{1}{2}$x2的共同点是( )
| A. | 开口向上,对称轴是y轴,顶点是原点 | |
| B. | 开口向下,对称轴是y轴,顶点是原点 | |
| C. | 对称轴是y轴,顶点是原点 | |
| D. | 函数y的最小值为0 |