Question

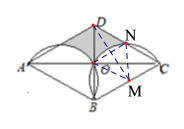
【题目】如图，菱形AD的边长为2，对角线AC、BD相交于点O，BD=2，分别以AB、BC为直径作半圆，则图中阴影部分的面积为__________．

Answer 1

【答案】－

【解析】

设BC的中点为M，CD交半圆M于点N，连接OM，MN．易证BCD是等边三角形，进而得∠OMN=60°，即可求出；再证四边形OMND是菱形，连接ON，MD，求出，利用，即可求解．

设BC的中点为M，CD交半圆M于点N，连接OM，MN．

∵四边形ABCD是菱形，

∴BD⊥AC，

∴两个半圆都经过点O，

∵BD=BC=CD=2，

∴BCD是等边三角形，

∴∠BCD=60°，

∴∠OCD=30°，

∴∠OMN=60°，

∴，

∵OD=OM=MN=CN=DN=1，

∴四边形OMND是菱形，

连接ON，MD，则MD⊥BC， OMN是等边三角形，

∴MD=CM=，ON=1，

∴MD×ON=，

∴．

故答是：－