题目内容
2.已知关于x的一元二次方程x2+x+k=0没有实数根,则k的取值范围是k<$\frac{1}{4}$.分析 根据根的判别式得出12-4×1×k<0,求出即可.
解答 解:∵关于x的一元二次方程x2+x+k=0没有实数根,
∴△<0,
即12-4×1×k<0,
解得:k<$\frac{1}{4}$,
故答案为:k<$\frac{1}{4}$.
点评 本题考查了解一元二次方程的根的判别式的应用,能正确理解根的判别式的内容是解此题的关键,注意:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0),当b2-4ac>0时,方程有两个不相等的实数根,当b2-4ac=0时,方程有两个相等的实数根,当b2-4ac<0时,方程没有实数根.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
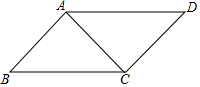 如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.