题目内容
关于x的方程ax2+bx+c=0的根为2和3，则方程ax2-bx-c=0的根为 ．
考点：根与系数的关系
专题：方程思想
分析：因为方程的两个根为2和3，所以方程可以方程因式为a（x-2）（x-3）=0，用含a的式子表示b和c，代入后面的方程可以用因式分解求出方程的根．
解答：解：∵ax2+bx+c=0的两根为2和3，
∴a（x-2）（x-3）=0，
整理得：ax2-5ax+6a=0，
∴b=-5a，c=6a．
把b，c代入方程ax2-bx-c=0，
得：ax2+5ax-6a=0，
a（x+6）（x-1）=0，
∴x1=-6，x2=1．
故答案是：-6和1．
∴a（x-2）（x-3）=0，
整理得：ax2-5ax+6a=0，
∴b=-5a，c=6a．
把b，c代入方程ax2-bx-c=0，
得：ax2+5ax-6a=0，
a（x+6）（x-1）=0，
∴x1=-6，x2=1．
故答案是：-6和1．
点评：本题考查的是用因式分解法解一元二次方程，把方程的两根代入方程，整理后用含a的式子表示b和c，然后把b，c代入后面的方程，用因式分解法可以求出方程的根．
练习册系列答案
相关题目
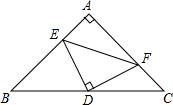如图，在等腰Rt△ABC中，D是斜边BC的中点，E在边AB上，F在边AC上，且∠EDF=90°．
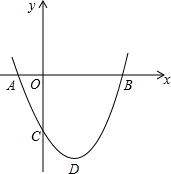如图，二次函数y=ax2+bx+c（a＞0）．图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为-1、3，与y轴负半轴交于点C．下面五个结论：①2a+b=0；②a+b+c＞0；③当x≤1时，y随x值的增大而增大；④当-1≤x≤3时，ax2+bx+c＜0；⑤只有当a=同时满足x：（x+y+1）=2y：（x+2y+3）和（3x+2y-xy）：（x+5y-2xy）=1：2的x，y为（ ）
A、x=
| ||||
B、x=-
| ||||
| C、x=7，y=35 | ||||
| D、x=1，y=5 |