题目内容
 如图,AB∥DE,BC∥EF,那么你能判断∠ABC与∠DEF的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗?与同伴交流.
如图,AB∥DE,BC∥EF,那么你能判断∠ABC与∠DEF的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗?与同伴交流.考点:平行线的性质
专题:
分析:首先根据两直线平行同位角相等可得∠B=∠DGC,∠E=∠DGC,再利用等量代换可得∠B=∠E;两个角的两边分别平行,那么这两个角相等或互补.
解答: 解:∠ABC=∠DEF,
解:∠ABC=∠DEF,
理由:∵AB∥DE,
∴∠B=∠DGC,
∵BC∥EF,
∴∠E=∠DGC,
∴∠B=∠E;
她的想法不对,两个角的两边分别平行,那么这两个角相等或互补;
理由:∵AB∥DE,
∴∠B+∠DGB=180°,
∵BC∥EF,
∴∠E=∠DGB,
∴∠B+∠E=180°.
 解:∠ABC=∠DEF,
解:∠ABC=∠DEF,理由:∵AB∥DE,
∴∠B=∠DGC,
∵BC∥EF,
∴∠E=∠DGC,
∴∠B=∠E;
她的想法不对,两个角的两边分别平行,那么这两个角相等或互补;
理由:∵AB∥DE,
∴∠B+∠DGB=180°,
∵BC∥EF,
∴∠E=∠DGB,
∴∠B+∠E=180°.
点评:此题主要考查了平行线的性质,关键是掌握两直线平行同位角相等.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
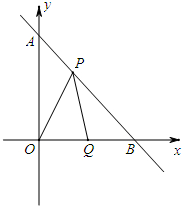 如图,直线y=-x+1与x轴,y轴分别交于A,B两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,交x轴于点Q.
如图,直线y=-x+1与x轴,y轴分别交于A,B两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,交x轴于点Q.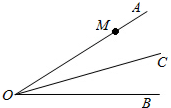 如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是
如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是 如图在⊙O中,弦AB和弦CD相交于点E,AB=CD,试探索BD和AC的大小关系,并证明.
如图在⊙O中,弦AB和弦CD相交于点E,AB=CD,试探索BD和AC的大小关系,并证明.