题目内容
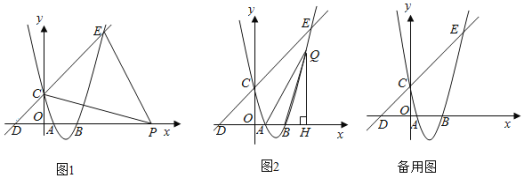
【题目】如图,已知双曲线y=![]() 和直线y=-x+2,P是双曲线第一象限上一动点,过P作y轴的平行线,交直线y=-x+2于Q点,O为坐标原点.
和直线y=-x+2,P是双曲线第一象限上一动点,过P作y轴的平行线,交直线y=-x+2于Q点,O为坐标原点.
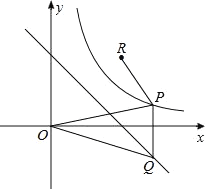

(1)求直线y=-x+2与坐标轴围成三角形的周长;
(2)设△PQO的面积为S,求S的最小值.
(3)设定点R(2,2),以点P为圆心,PR为半径画⊙P,设⊙P与直线y=-x+2交于M、N两点.
①判断点Q与⊙P的位置关系,并说明理由;
②求S△MON=S△PMN时的P点坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)①点
;(3)①点![]() 在
在![]() 上,理由见解析;②
上,理由见解析;②![]() 或
或![]() .
.
【解析】
(1)先求直线y=-x+2与坐标轴的交点A,B坐标,利用勾股定理求AB,即可得△OAB的周长。
(2)设![]() ,即可得出S=
,即可得出S=![]() ,利用二次函数最值即可求得
,利用二次函数最值即可求得![]()
(3)①利用勾股定理或两点之间距离公式可求得PR2和PQ2,由PQ=PR,可得点Q在⊙P上;
②根据等腰直角三角形性质可得OE=![]() ,PD=
,PD=![]() ,再由
,再由![]() ,可得OE=PD,进而可得
,可得OE=PD,进而可得![]() ,从而可求得点P的坐标。
,从而可求得点P的坐标。
解:(1)如图,在![]() 中,令
中,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∴![]() 的周长
的周长![]()
![]() ;
;
(2)设![]()
![]() ,则
,则![]() ,
,
∴![]()
∴![]()
∴当![]() 时,
时,![]() ;
;
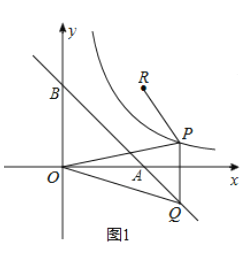
(3)①点![]() 在
在![]() 上.如图2,设
上.如图2,设![]()
![]() ,
,
由(2)知![]() ,
,
∴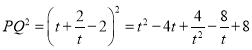
过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,
轴,
![]() 与
与![]() 交于
交于![]() ,则
,则![]()
∴![]() ,
,![]()
∴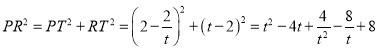
∴![]()
∴![]()
∴点![]() 在
在![]() 上;
上;

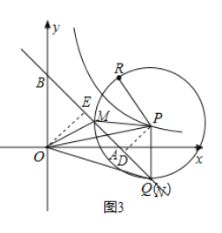
②如图3,过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,则
,则![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,
∵![]() 轴
轴
∴![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 或
或![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目