题目内容
 如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=
如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=| k |
| x |
①若k=4,则△OEF的面积为
| 8 |
| 3 |
②若k=
| 21 |
| 8 |
③满足题设的k的取值范围是0<k≤12;
④若DE•EG=
| 25 |
| 12 |
其中正确的命题的序号是
考点:反比例函数综合题,勾股定理
专题:压轴题,数形结合,待定系数法
分析:(1)若k=4,则计算S△OEF=
≠
,故命题①错误;
(2)如答图所示,若k=
,可证明直线EF是线段CN的垂直平分线,故命题②正确;
(3)因为点F不经过点C(4,3),所以k≠12,故命题③错误;
(4)求出直线EF的解析式,得到点D、G的坐标,然后求出线段DE、EG的长度;利用算式DE•EG=
,求出k=1,故命题④正确.
| 16 |
| 3 |
| 8 |
| 3 |
(2)如答图所示,若k=
| 21 |
| 8 |
(3)因为点F不经过点C(4,3),所以k≠12,故命题③错误;
(4)求出直线EF的解析式,得到点D、G的坐标,然后求出线段DE、EG的长度;利用算式DE•EG=
| 25 |
| 12 |
解答:解:命题①错误.理由如下:
∵k=4,
∴E(
,3),F(4,1),
∴CE=4-
=
,CF=3-1=2.
∴S△OEF=S矩形AOBC-S△AOE-S△BOF-S△CEF
=S矩形AOBC-
OA•AE-
OB•BF-
CE•CF
=4×3-
×3×
-
×4×1-
×
×2=12-2-2-
=
,
∴S△OEF≠
,故命题①错误;
命题②正确.理由如下:
∵k=
,
∴E(
,3),F(4,
),
∴CE=4-
=
,CF=3-
=
.
如答图,过点E作EM⊥x轴于点M,则EM=3,OM=
;
在线段BM上取一点N,使得EN=CE=
,连接NF.

在Rt△EMN中,由勾股定理得:MN=
=
=
,
∴BN=OB-OM-MN=4-
-
=
.
在Rt△BFN中,由勾股定理得:NF=
=
=
.
∴NF=CF,
又∵EN=CE,
∴直线EF为线段CN的垂直平分线,即点N与点C关于直线EF对称,
故命题②正确;
命题③错误.理由如下:
由题意,点F与点C(4,3)不重合,所以k≠4×3=12,故命题③错误;
命题④正确.理由如下:
为简化计算,不妨设k=12m,则E(4m,3),F(4,3m).
设直线EF的解析式为y=ax+b,则有
,解得
,
∴y=-
x+3m+3.
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答图,过点E作EM⊥x轴于点M,则OM=AE=4m,EM=3.
在Rt△ADE中,AD=OD-OA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OG-OM=(4m+4)-4m=4,EM=3,由勾股定理得:EG=5.
∴DE•EG=5m×5=25m=
,解得m=
,
∴k=12m=1,故命题④正确.
综上所述,正确的命题是:②④,
故答案为:②④.
∵k=4,
∴E(
| 4 |
| 3 |
∴CE=4-
| 4 |
| 3 |
| 8 |
| 3 |
∴S△OEF=S矩形AOBC-S△AOE-S△BOF-S△CEF
=S矩形AOBC-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4×3-
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 16 |
| 3 |
∴S△OEF≠
| 8 |
| 3 |
命题②正确.理由如下:
∵k=
| 21 |
| 8 |
∴E(
| 7 |
| 8 |
| 21 |
| 32 |
∴CE=4-
| 7 |
| 8 |
| 25 |
| 8 |
| 21 |
| 32 |
| 75 |
| 32 |
如答图,过点E作EM⊥x轴于点M,则EM=3,OM=
| 7 |
| 8 |
在线段BM上取一点N,使得EN=CE=
| 25 |
| 8 |

在Rt△EMN中,由勾股定理得:MN=
| EN2-EM2 |
(
|
| 7 |
| 8 |
∴BN=OB-OM-MN=4-
| 7 |
| 8 |
| 7 |
| 8 |
| 9 |
| 4 |
在Rt△BFN中,由勾股定理得:NF=
| BN2+BF2 |
(
|
| 75 |
| 32 |
∴NF=CF,
又∵EN=CE,
∴直线EF为线段CN的垂直平分线,即点N与点C关于直线EF对称,
故命题②正确;
命题③错误.理由如下:
由题意,点F与点C(4,3)不重合,所以k≠4×3=12,故命题③错误;
命题④正确.理由如下:
为简化计算,不妨设k=12m,则E(4m,3),F(4,3m).
设直线EF的解析式为y=ax+b,则有
|
|
∴y=-
| 3 |
| 4 |
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答图,过点E作EM⊥x轴于点M,则OM=AE=4m,EM=3.
在Rt△ADE中,AD=OD-OA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OG-OM=(4m+4)-4m=4,EM=3,由勾股定理得:EG=5.
∴DE•EG=5m×5=25m=
| 25 |
| 12 |
| 1 |
| 12 |
∴k=12m=1,故命题④正确.
综上所述,正确的命题是:②④,
故答案为:②④.
点评:本题综合考查了函数的图象与性质、反比例函数图象上点的坐标特征、比例系数k的几何意义、待定系数法、矩形及勾股定理等多个知识点,有一定的难度.本题计算量较大,解题过程中注意认真计算.

练习册系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc<0;②b2-4ac>0;③3a+c<0;④16a+4b+c>0.
其中正确结论的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列几何体的主视图、俯视图和左视图都是长方形的是( )
A、 |
B、 |
C、 |
D、 |

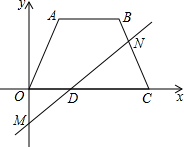 如图,在平面直角坐标系中,梯形OABC各顶点的坐标分别为O(0,0),A(2,3),B(4,3),C(6,0).点M的坐标为(0,-1),D是线段OC上的一个动点,当D点从O点向C点移动时,直线MD与梯形的一边交于点N.设点D的横坐标为t.
如图,在平面直角坐标系中,梯形OABC各顶点的坐标分别为O(0,0),A(2,3),B(4,3),C(6,0).点M的坐标为(0,-1),D是线段OC上的一个动点,当D点从O点向C点移动时,直线MD与梯形的一边交于点N.设点D的横坐标为t. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.