题目内容
16．
如图：已知等腰三角形ACB和ECD，找出图中的全等三角形并证明．
分析 根据等腰直角三角形的性质得出∠ACB=∠BCE=90°，AC=BC，CD=CE，然后根据SAS即可证得△ACE≌△BCD．
解答 解：∵△ACB和△ECD是等腰直角三角形，
∴∠ACB=∠BCE=90°，AC=BC，CD=CE，
在△ACE和△BCD中，
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD=90°}\\{CE=CD}\end{array}\right.$
∴△ACE≌△BCD（SAS）．
点评 本题考查了等腰直角三角形的性质和全等三角形的判定，熟练掌握性质定理是解题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
如图，已知边长为6的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC，则CE的长是24-12$\sqrt{3}$．
4．
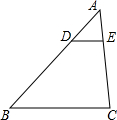如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）
如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）| A． | $\frac{AE}{EC}=\frac{1}{2}$ | B． | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| C． | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{2}$ | D． | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ |